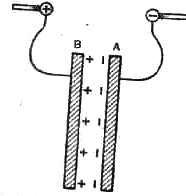
Уравнение движения ротора генератора. Абсолютное и относительное движение ротора. Физический смысл входящих в него величин
В процессе работы генератора к его ротору приложены два момента: вращающий момент турбины МТ и электромагнитный момент М, пропорциональный отдаваемой генератором активной мощности Р и являющийся моментом сопротивления для турбины
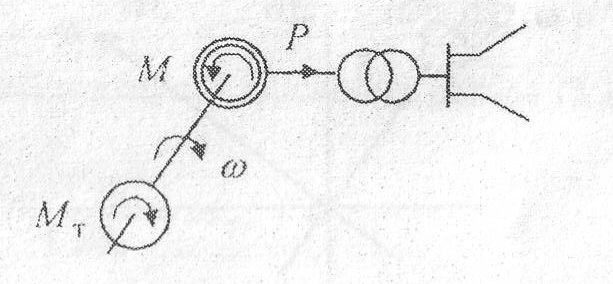
При несоответствии этих моментов скорость ротора генератора изменяется в соответствии со вторым законом Ньютона  (1)
(1)
где J — осевой момент инерции вращающихся масс роторов генератора и турбины, кг-м 2 ;
Q — скорость вращения роторов в механическом движении, рад*с -1 ;
МТ, М — моменты, действующие на ротор генератора, Н-м.
Уравнение абсолютного движения ротора (1) в относительных единицах примет вид:  . Здесь
. Здесь  .
. 
 — постоянная инерции, равна времени разгона tразг ротора отключенного от сети генератора от состояния покоя до номинальной скорости вращения при приложении номинального момента турбины.
— постоянная инерции, равна времени разгона tразг ротора отключенного от сети генератора от состояния покоя до номинальной скорости вращения при приложении номинального момента турбины.
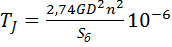 , c
, c
n – скорость ротора
Sб – базисная мощность
GD 2 – маховый момент
Уравнение относительного движения ротора 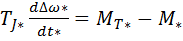 .
.
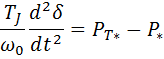
19. Наиболее точным описанием переходных процессов в синхронном двигателе являются уравнения Парка-Горева. Учитывая, что двигатель в отличие от генератора потребляет электрическую энергию и момент, развиваемый двигателем, является вращающим моментом.

Уравнение движения ротора двигателя 
В общем случае момент сопротивления механизма, присоединенного к ротору двигателя Ммех, зависит от скорости вращения. Часто полагают

где Мст -момент сопротивления механизма при скорости ϖ=0 (статический момент);
MQ -момент сопротивления механизма при номинальной скорости вращения ϖ0
а — коэффициент, обычно равный 0-2.
Полные уравнения Парка-Горева для описания переходных процессов в синхронных двигателях при исследований устойчивости электрических систем применяются редко. Обычно используются упрощенные уравнения. Упрощение уравнений Парка-Горева для синхронного двигателя осуществляется точно так же, как и для синхронного генератора. При этом, как и для синхронного генератора, для синхронного двигателя имеется несколько математических моделей, характеризующихся различной степенью точности описания переходных процессов.
20. Что собою обозначают (как введены) величины: Eq, E’q,E”q,E”d,E”
 -ЭДС возбуждения пропорционально полному току ротора
-ЭДС возбуждения пропорционально полному току ротора
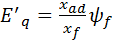 -переходная ЭДС по оси q-пропорционально результирующему потокосцеплению обмотки возбуждения
-переходная ЭДС по оси q-пропорционально результирующему потокосцеплению обмотки возбуждения 
 для явнополюсных генераторов
для явнополюсных генераторов
 для неявнополюсных генераторов
для неявнополюсных генераторов
Уравнение движения ротора генератора
В процессе эксплуатации СЭС балансы мощности турбин и генераторов, электроприводов и нагрузок периодически нарушаются. Это происходит из-за несовпадения реального графика нагрузки с планируемым. С учетом принятых допущений уравнение баланса мощности для отдельного агрегата турбина-генератор в относительных единицах можно записать в виде
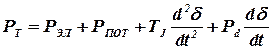 , (2.5)
, (2.5)
где РТ– мощность турбины, определяющая исходный установившийся режим системы (РО = РТ = РЭЛ);
РЭЛ – электромагнитная мощность генератора;
РПОТ – механические потери в агрегате;
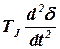 — избыточный момент на валу генератора;
— избыточный момент на валу генератора;
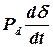 — потери в демпферных обмотках при нарушении;
— потери в демпферных обмотках при нарушении;
Рd – демпферный коэффициент;
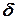 — , угол, определяющий пространственное положение продольной оси ротора;
— , угол, определяющий пространственное положение продольной оси ротора;
ТJ– постоянная инерции вращающихся масс турбины и генератора.
ТJ— время, в течение которого скорость ротора изменяется от нуля до номинальной под действием номинального избыточного момента и при постоянном моменте сопротивления. Она определяется следующим образом:
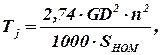 (2.6)
(2.6)
где GD 2 — маховой момент, т·м 2 ,
G – масса подвижных элементов;
D – диаметр подвижных масс;
п – скорость вращения, об/мин;
SНОМ – номинальная мощность генератора, кВ·А.
Выражение (2.5) называется уравнением электромеханических переходных процессов. Если потерями мощности в агрегате и потерями в демпферных контурах пренебречь, то это уравнение примет вид
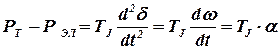 , (2.7)
, (2.7)
где ω — угловая скорость;
α — угловое ускорение вращающихся масс.
При РТ – РЭЛ РТ) имеет место тормозящий момент на валу агрегата, а при РТ–РЭЛ>0 (РТ > РЭЛ) — ускоряющий момент.
Торможение или ускорения роторов генераторов являются следствием набросов и сбросов нагрузки. Возникающий при этом небаланс мощности покрывается за счет энергии вращающихся масс.
Мощность, развиваемая турбиной, зависит от массы пропускаемого через нее пара или воды в единицу времени и может изменяться с помощью первичных регуляторов.
Незначительное возмущение в цепи статора генератора вызывает движение ротора в сторону увеличения или уменьшения угла δ (это зависит от знака избыточного момента). Возмущение сообщает ротору некоторое ускорение α, которое в относительных единицах пропорционально избыточному моменту ΔМ и обратно пропорционально постоянной инерции Тj:
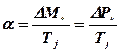 . (2.8)
. (2.8)
Здесь принимается, что при небольших изменениях скорости ΔM*=ΔР*;
Возвращаясь к уравнению (2.6) и учитывая, что ускорение представляет собой не что иное, как вторую производную от угла по времени
 , (2.9)
, (2.9)
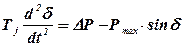 , (2.10)
, (2.10)
где Р0 — мощность турбины;
Ртах — максимальное значение мощности аварийного режима.
Уравнение (2.5) также называется уравнением движения ротора генератора. Его решение в форме δ = f(t) дает картину изменения угла δ во времени и позволяет судить об устойчивости генератора.
Глава 3. ДИНАМИЧЕСКАЯ УСТОЙЧИВОСТЬ
Если статическая устойчивость характеризует установившийся режим системы, то при анализе динамической устойчивости выявляется способность системы сохранять синхронный режим работы при больших его возмущениях. Большие возмущения возникают при различных коротких замыканиях, отключении линии электропередачи, генераторов, трансформаторов и т.д. К большим возмущениям относятся также изменения мощности крупной нагрузки, потеря возбуждения какого-либо генератора, включение крупных двигателей. Одним из следствий возникшего возмущения является отклонение скоростей вращения роторов генераторов от синхронной (качания роторов генераторов системы).
Если после какого-либо возмущения взаимные углы роторов примут определенные значения (их колебания затухнут около каких-либо новых значений), то считается, что динамическая устойчивость сохраняется. Если хотя бы у одного генератора ротор начинает проворачиваться относительно поля статора, то это признак нарушения динамической устойчивости. В общем случае о динамической устойчивости системы можно судить по зависимостям δ = f(t),полученным в результате совместного решения уравнений движения роторов генераторов. Но существует более простой и наглядный метод оценки динамической устойчивости, основанный на энергетическом подходе к анализу динамической устойчивости, который называется графическим методом или методом площадей.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Русские Блоги
Момент инерции и уравнение движения ротора синхронного генератора (1) Основные физические понятия
Момент инерции и уравнение движения ротора синхронного генератора (1) Основные физические понятия
1.1 Момент инерции
Момент инерции также называется моментом инерции (момент инерции), обычно в терминахJУказывает, что размер по Международной системе единиц составляет [кг · м 2 ]. Момент инерции — это мера инерции объекта по отношению к его вращательному движению. Момент инерции твердого тела относительно определенной оси вращения определяет момент, необходимый объекту для выполнения движения с определенным угловым ускорением вокруг оси вращения. Роль момента инерции в динамике вращения эквивалентна массе в линейной динамике, описывающей взаимосвязь между несколькими физическими величинами, такими как угловой момент, угловая скорость, крутящий момент и угловое ускорение.
def.1 Момент инерции
| Размер проблемы | Качество Micro |
|---|---|
| Качество линий (одномерные объекты, например стержни и т. Д.) | d m = λ d l dm = λdl d m = λ d l |
| Качество поверхности (двухмерные объекты, такие как тонкие пластины и т. Д.) | d m = σ d s dm = σds d m = σ d s |
| Масса тела (трехмерные объекты, такие как сферы и т. Д.) | d m = ρ d V dm = ρdV d m = ρ d V |
def.2 Кинетическая энергия вращения
1.2 Крутящий момент
Сила, которая заставляет объект вращаться вокруг оси вращения или точки опоры, называется крутящим моментом, который также называется крутящим моментом. Следовательно, в нормально работающем синхронном генераторе крутящий момент более уместно выражать как крутящий момент. Толкание или тяга требует силы, а кручение — момента. Момент равен радиальному векторуrИ силаFВнешний продукт.
def.3 Момент
Момент равен силе, действующей на рычагFУмножьте вертикальное расстояние от точки опоры на силу. Кроме того, момент силы является вектором, и его направление: в том же направлении, что и ось вращения вызываемого им вращательного движения. Направление момента можно определить по правилу правой руки: правая плоскость перпендикулярна радиальному векторуrИ силаFОпределяемая плоскость, четыре пальца от радиального вектораrСилаFВозьми его, тогда большой палец указывает на моментTНаправление. На рисунке ниже показано, как определить крутящий момент с помощью правила правой руки.T, Радиальный векторr, СилаFВзаимосвязь пространственного положения между (рисунок из Википедии).

Предполагая силуFДействующий на должностиrО частицах. Если источник выбран в качестве опорной точки, крутящий моментTОпределяется как:
T ⃗ = r ⃗ × F ⃗ vec T = vec r times vec F T
Величина крутящего момента T равна:
T = ∣ r ⃗ ∣ ⋅ ∣ F ⃗ ∣ ⋅ s i n θ T = |vec r|·|vec F|·sinθ T = ∣ r
∣ ⋅ s i n θ
Согласно Международной системе единиц крутящий моментTРазмер составляет [Н · м] = [кг · м 2 ·s −2 ]. среди них,θРадиальный векторrИ силаFУгол между.
1.3 Угловой момент
В физике угловой момент — это физическая величина, связанная с вектором положения и импульсом объекта. Для начала O инерциальной системы отсчета угловой момент объекта является внешним произведением его вектора положения и импульса. Следовательно, угловой момент L также является вектором, обычно записываемым как:
L ⃗ = r ⃗ × p ⃗ vec L = vec r times vec p L
где,rПредставляет радиальный вектор объекта,pПредставляет импульс,LПредставляет угловой момент. Поскольку импульс выражается как:
p ⃗ = m v ⃗ vec p = m vec v p
иvПредставляет касательную скорость материальной точки во время вращения, поэтому:
ω ⃗ = r ⃗ × v ⃗ ∣ r ⃗ ∣ 2 vec ω = frac <|vec r|^2>ω
Итак, конечный угловой моментLТакже может быть записано как:
L ⃗ = r ⃗ × p ⃗ = r ⃗ × [ m ( ω ⃗ × r ⃗ ) ] = m ω ⃗ ∣ r ⃗ ∣ 2 = m r 2 ω ⃗ = J ω ⃗ vec L = vec r times vec p = vec r times [m(vec ω times vec r)] = m vec ω |vec r|^2 = mr^2 vec ω = J vec ω L
где,JПредставляет момент инерции материальной точки,ωВектор угловой скорости. Очевидно, угловой моментLРазмер составляет [кг · м 2 ·s -1 ]。
Предполагая, что сумма внешних моментов, действующих на объект, равна нулю, угловой момент объекта сохраняется, то есть принцип сохранения момента количества движения. Следует отметить, что из-за различных условий, сохраняется ли угловой момент, не напрямую связано с тем, сохраняется ли импульс.
1.4 Связь между крутящим моментом, угловым моментом, энергией и мощностью
1.4.1 Связь между крутящим моментом и угловым моментом
В области классической механики один и тот же объект имеет определенный импульс в определенной системе отсчета, а значение количества движения зависит от значения двух физических величин: массы движущегося объекта в системе отсчета.mСо скоростьюv. В физике импульс определяется следующим образом:
p ⃗ = m v ⃗ vec p = m vec v p
Найдите первую производную импульса по времени и получите:
d p ⃗ d t = m d v ⃗ d t + v ⃗ d m d t frac = m frac + vec v frac d t d p
d t d m
Это наиболее точное выражение, качествоmНа высоких скоростях (близких к скорости света) она будет увеличиваться из-за влияния теории относительности, но мы обычно изучаем проблемы только на низких скоростях, поэтому мы приближаем:
v ⃗ d m d t ≈ 0 ⃗ vec v frac approx vec 0 v
Следовательно, в некотором смысле следующая формула, которую мы обычно изучаем, упрощена:
d p ⃗ d t = m d v ⃗ d t = m a ⃗ = F ⃗ frac = m frac = m vec a = vec F d t d p
То есть силаFИмпульсpСкорость изменения.
Между крутящим моментом и угловым моментом существует аналогичная связь. Предположим, что вектор положения частицы относительно начала координат равенr, Импульсp. Выберите начало координат в качестве точки отсчета, угловой момент этой частицы равенL:
L ⃗ = r ⃗ × p ⃗ vec L = vec r times vec p L
Угловой момент частицыLПравильное времяtПроизводная от:
d L ⃗ d t = r ⃗ × d p ⃗ d t + p ⃗ × d r ⃗ d t = m r ⃗ × d v ⃗ d t + m v ⃗ × v ⃗ = r ⃗ × m a ⃗ frac = vec r times frac + vec p times frac = m vec r times frac + m vec v times vec v = vec r times m vec a d t d L
И определение крутящего момента T:
T ⃗ = r ⃗ × F ⃗ vec T = vec r times vec F T
Таким образом, можно видеть, что, подобно соотношению «импульс-сила», соотношение «угловой момент-момент» одновременно удовлетворяет:
d L ⃗ d t = T ⃗ frac = vec T d t d L
— крутящий моментTУгловой моментLПроизводная по времени. Далее можно вывести:
T ⃗ = J d ω ⃗ d t vec T = J frac T
1.4.2 Взаимосвязь между крутящим моментом, энергией и мощностью
Предполагая силуFК объекту заставьте объект переместиться на определенное смещениеs, Сила выполняет механическую работу с объектомW. Точно так же предположим, что к объекту приложен момент, заставляющий объект вращаться за счет углового смещения, тогда этот момент выполняет механическую работу с объектом. Для вращательного движения неподвижной оси, проходящей через центр масс, математическое уравнение выражается как:
W = ∫ θ 1 θ 2 T d θ W = int_<θ_1 >^ <θ_2>Tdθ W = ∫ θ 1 θ 2 T d θ
где,WМеханическая работа,θ1、θ2Это начальный угол и конечный угол. Пока властьPЯвляется производной механической работы по времени. Следовательно, для вращательного движения должно быть:
P = d W d t = T ⃗ ⋅ ω ⃗ P = frac = vec T · vec ω P = d t d W = T
Обратите внимание, что крутящий моментTВводимая мощность связана только с мгновенной угловой скоростью, и независимо от того, увеличивается ли угловая скорость, уменьшается или остается неизменной, мощность не имеет никакого отношения к этим условиям.
На рисунке ниже показан крутящий момент.T,Угловой моментL, СилаF, импульсp, Вектор положенияrВзаимосвязь пространственного положения между (рисунок из Википедии).

1.5 Размер! измерение! ! измерение! ! !
Вышеупомянутая формула получена под хорошо известным значением, поэтому особое внимание следует уделить проблеме размерности. Хотя есть некоторые клише, если вы не разъясняете физическое отношение под известным значением здесь, вы можете использовать формулу под стандартным значением единицы (то есть содержание, обсуждаемое в следующей статье, хотя, возможно, уже слишком поздно писать . ) Делайте различные ошибки, поэтому эти единицы можно резюмировать следующим образом.
Уравнение движения ротора синхронного генератора
Воропаев Е.Г.
Электротехника
Если в рассмотренных выше асинхронных машинах ротор имел частоту вращения, отличную от частоты вращения магнитного поля статора, то в синхронных эти частоты равны между собой.
Синхронные машины могут работать как генераторами, так и двигателями.
В зависимости от типа привода синхронные генераторы получили и свои названия.
Турбогенератор, например, — это генератор, приводимый в движение паровой турбиной, гидрогенератор вращает водяное колесо, а дизель — генератор механически связан с двигателем внутреннего сгорания.
Синхронные двигатели широко применяют для привода мощных компрессоров, насосов, вентиляторов.
Синхронные микродвигатели используют для привода лентопротяжных механизмов регистрирующих приборов, магнитофонов и т.д.
6.1. КОНСТРУКЦИЯ И ПРИНЦИП ДЕЙСТВИЯ СИНХРОННОГО ГЕНЕРАТОРА
Статор синхронной машины по конструкции не отличается от статора асинхронного двигателя. В пазах статора размещается трехфазная, двухфазная или однофазная обмотки.
Заметное отличие имеет ротор, который принципиально представляет собой постоянный магнит или электромагнит.
Это налагает особые требования на геометрическую форму ротора. Любой магнит имеет полюса, число которых может быть два и более.
На рис. 6.1.1 приведены две конструкции генераторов, с тихоходным и быстроходным ротором.

Быстроходными бывают, как правило, турбогенераторы. Количество пар магнитных полюсов у них равно единице. Чтобы такой генератор вырабатывал электрический ток стандартной частоты f = 50 Гц, его необходимо вращать с частотой

На гидроэлектростанциях вращение ротора зависит от движения водяного потока. Но и при медленном вращении такой генератор должен вырабатывать электрический ток стандартной частоты f = 50 Гц.
Поэтому для каждой гидроэлектростанции конструируется свой генератор, на определенное число магнитных полюсов на роторе.
В качестве примера приведем параметры синхронного генератора, работающего на Днепровской ГЭС.
Водяной поток вращает ротор генератора с частотой n = 33,3 об / мин. Задавшись частотой f = 50 Гц, определим число пар полюсов на роторе:

Принцип действия синхронного генератора основан на явлении электромагнитной индукции. Ротор с магнитными полюсами создает вращающееся магнитное поле, кото-рое, пересекая обмотку статора, наводит в ней ЭДС. При подключении к генератору нагрузки генератор будет являться источником переменного тока.
6.2. ЭДС СИНХРОННОГО ГЕНЕРАТОРА
Как было показано выше, величина наводимой в обмотке статора ЭДС количественно связана с числом витков обмотки и скорости изменения магнитного потока:

Переходя к действующим значениям, выражение ЭДС можно записать в виде:

где n — частота вращения ротора генератора,
Ф — магнитный поток,
c — постоянный коэффициент.
При подключении нагрузки напряжение на зажимах генератора в разной степени меняется. Так, увеличение активной нагрузки не оказывает заметного влияния на напряжение. В то же время индуктивная и емкостная нагрузки влияют на выходное на-пряжение генератора. В первом случае рост нагрузки размагничивает генератор и снижает напряжение, во втором происходит его подмагничивание и повышение напряжения. Такое явление называется реакцией якоря.
Для обеспечения стабильности выходного напряжения генератора необходимо регулировать магнитный поток. При его ослаблении машину надо подмагнитить, при увеличении — размагнитить. Делается это путем регулирования тока, подаваемого в обмотку возбуждения ротора генератора.
6.3. СИНХРОННЫЙ ДВИГАТЕЛЬ
6.3.1. КОНСТРУКЦИЯ И ПРИНЦИП ДЕЙСТВИЯ
Конструкция синхронного двигателя такая же, как и у синхронного генератора.
При подаче тока в трехфазную обмотку статора в нем возникает вращающееся магнитное поле. Частота вращения его определяется формулой:

где f — частота тока питающей сети,
р — число пар полюсов на статоре.
Ротор, являющийся часто электромагнитом, будет строго следовать за вращаю-щимся магнитным полем, т.е. его частота вращения n2 = n1.
Рассмотрим принцип действия синхронного двигателя на следующей условной модели (рис. 6.3.1.). Пусть магнитное поле статора будет смоделировано системой вращающихся магнитных полюсов N — S.

Ротор двигателя тоже представляет собой систему электромагнитов S — N, кото-рые «сцеплены» с полюсами на статоре. Если нагрузка на двигателе отсутствует, то оси полюсов статора будут совпадать с осями полюсов ротора (  = 0).
= 0).
Если же к ротору подключена механическая нагрузка, то оси полюсов статора и ротора могут расходиться на некоторый угол  .
.
Однако «магнитное сцепление» ротора со статором будет продолжаться, и частота вращения ротора будет равна синхронной частоте статора (n2 = n1). При больших значениях ротор может выйти из «сцепления» и двигатель остановится.
Главное преимущество синхронного двигателя перед асинхронным — это обеспечение синхронной скорости вращения ротора при значительных колебаниях нагрузки.
6.3.2. СИСТЕМА ПУСКА СИНХРОННОГО ДВИГАТЕЛЯ
Как мы показали выше, синхронное вращение ротора обеспечивается «магнитным сцеплением» полюсов ротора с вращающимся магнитным полем статора.
В первый момент пуска двигателя вращающееся магнитное поле статора возникает практически мгновенно. Ротор же, обладая значительной инерционной массой, прийти в синхронное вращение сразу не сможет. Его надо «разогнать» до подсинхронной скорости каким-то дополнительным устройством.
Долгое время роль разгонного двигателя играл обычный асинхронный двигатель, механически соединенный с синхронным.
Ротор синхронного двигателя приводится во вращение до подсинхронной скорости. Далее двигатель сам втягивается в синхронизм.
Обычно мощность пускового двигателя составляет 5-15 % от мощности синхронного двигателя. Это позволяет пускать в ход синхронный двигатель только вхолостую или при малой нагрузке на валу.
Применение пускового двигателя мощностью, достаточной для пуска синхронного двигателя под нагрузкой делает такую установку громоздкой и дорогой.
В последнее время используется так называемая система асинхронного пуска синхронных двигателей. С этой целью в полюсные наконечники забивают стержни, напоминающие собою короткозамкнутую обмотку асинхронного двигателя (рис. 6.3.2.1).

В начальный период пуска синхронный двигатель работает как асинхронный, а в последующем — как синхронный. В целях безопасности обмотку возбуждения в начальном периоде пуска закорачивают, а на заключительном подключают к источнику по-стоянного тока.
6.4. РЕАКТИВНЫЙ СИНХРОННЫЙ ДВИГАТЕЛЬ
В лабораторной практике, в быту и в маломощных механизмах применяют так называемые реактивные синхронные двигатели.
От обычных классических машин они отличаются лишь конструкцией ротора. Ротор здесь не является магнитом или электромагнитом, хотя по форме напоминает собой полюсную систему.
Принцип действия реактивного синхронного двигателя отличен от рассмотренного выше. Здесь работа двигателя основана, на свободной ориентации ротора таким образом, чтобы обеспечить магнитному потоку статора лучшую магнитную проводимость (рис. 6.4.1).

Действительно, если в какой-то момент времени максимальный магнитный поток будет в фазе А — X, то ротор займет положение вдоль потока ФА. Через 1/3 периода максимальным будет поток в фазе В — У. Тогда ротор развернется вдоль потока ФВ. Еще через 1/3 периода произойдет ориентация ротора вдоль потока. ФС. Так непрерывно и синхронно ротор будет вращаться с вращающимся магнитным полем статора.
В школьной практике иногда, при отсутствии специальных синхронных двигателей, возникает необходимость в синхронной передаче.
Эту проблему можно решить с помощью обычного асинхронного двигателя, если придать ротору следующую геометрическую форму (рис. 6.4.2).

6.5. ШАГОВЫЙ ДВИГАТЕЛЬ
Этот тип двигателя является машиной постоянного тока, хотя принцип действия его напоминает синхронный реактивный двигатель.
Как видно из рис. 6.5.1, статор двигателя имеет шесть пар выступающих полюсов.

Каждые две катушки, расположенные на противоположных полюсах статора, образуют обмотку управления, включаемую, в сеть постоянного тока. Ротор — двухполюсный.
Если подключить к источнику постоянного тока катушки полюсов 1 — 1′, то ротор расположится вдоль этих полюсов. Если задействовать катушки полюсов 2 — 2′, а ка-тушки полюсов 1 — 1′ обесточить, то ротор повернется и займет положение вдоль полю-сов 2 — 2′. Такой же поворот ротора произойдет, если включить в сеть катушки полюсов 3 — 3′. Так, шагами, ротор будет «следовать» за своей обмоткой управления.
Преимуществом шаговых двигателей является то, что в них совершенно отсутствует «самоход». Они поворачиваются и строго фиксируются с шагом, пропорциональ-ным числу полюсов на статоре. Это качество делает его незаменимым в особо точных механизмах (для привода часов, механизмов подачи ядерного топлива в реакторах, в станках с ЧПУ и т.д.).
Управление шаговыми двигателями ведется с применением различных электронных устройств (триггеров Шмидта и др.).
6.6. КОЛЛЕКТОРНЫЙ ДВИГАТЕЛЬ ПЕРЕМЕННОГО ТОКА
Безколлекторные асинхронные и синхронные двигатели при многих положительных качествах имеют существенные недостатки. Они не допускают достаточно плавного и экономичного регулирования вращения.
Этот пробел частично восполняют коллекторные двигатели переменного тока.
Коллекторные двигатели бывают однофазными и трехфазными.
Ротор однофазного коллекторного двигателя выполнен в виде цилиндра с фазными обмотками, статор — явнополюсный.
Так как обмотка полюсов статора, подключаемая к сети переменного тока, создает пульсирующее магнитное поле, то все элементы магнитной цепи машины набираются из отдельных листов электротехнической стали.
Вращающий момент в однофазном коллекторном двигателе создается взаимодействием токов в обмотке ротора с магнитным потоком полюсов. На рис. 6.6.1- показана схема подключения к сети коллекторного двигателя.

Коллекторные двигатели могут работать как от сети переменного тока, так и от сети постоянного тока. Это обстоятельство послужило для присвоения им наименования универсальных коллекторных двигателей. Коллекторные двигатели широко при-меняются для привода швейных машин, пылесоса и т.д.
3.2. Уравнение движения ротора синхронной машины
В наиболее общем виде уравнение движения ротора синхронной машины будет представляться в соответствии со вторым законом Ньютона в следующем виде
 , (3.1)
, (3.1)
где J– момент инерции ротора агрегата: турбины и генератора; ω – угловая скорость вращения ротора генератора, которая может рассматриваться как сумма синхронной угловой скорости вращения ротора ω0 и скорости перемещения ротора относительно синхронно вращающейся оси Δω, т. е. ω = ωо + Δω; Mт – момент, создаваемый турбиной, который имеет вращательный характер; М– электромагнитный момент на валу ротора генератора, несущий тормозящий характер.
Переходный процесс в соответствии с данным выражением можно характеризовать отклонениями координат Δω, ΔMт, ΔM от их нормальных установившихся значений: ω0, Mто, Mо. Для системы, содержащей n число синхронных машин, таких уравнений (3.1) также будет n.
В нормальном установившемся режиме угловая скорость ω = ωо = const, а также Mт = Mо . Для отклонений координат Δω , ΔMт , ΔM, т. е. для анализа переходного процесса, уравнение движения ротора (3.1) сохраняет свою структуру и принимает следующий вид
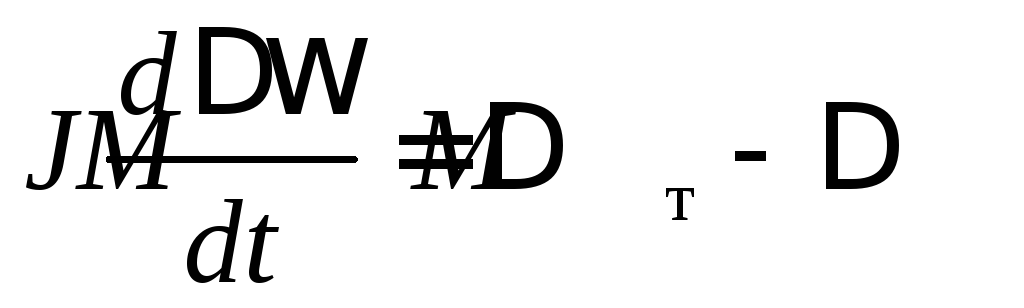 (3.2)
(3.2)
 . (3.3)
. (3.3)
В неподвижной системе координат положение ротора синхронной машины в каждый момент времени можно характеризовать некоторым положением угла γ, который отсчитывается между поперечной осью синхронной машины q и магнитной осью статорной обмотки фазы А: γ = (q^А). И
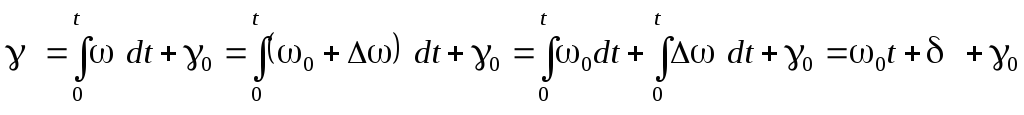 (3.4)
(3.4)
Здесь угол δ отсчитывается от оси, которая вращается с постоянной угловой скоростью исходного установившегося режима ωо и называется синхронно вращающейся осью. Обычно также угол δ называют еще абсолютным углом. Разность этих абсолютных углов для любой пары синхронных машин образует относительные или взаимные углы: 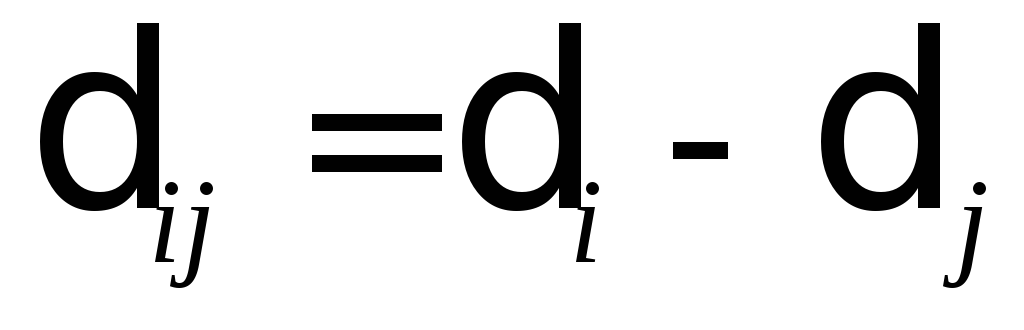 . Поскольку
. Поскольку
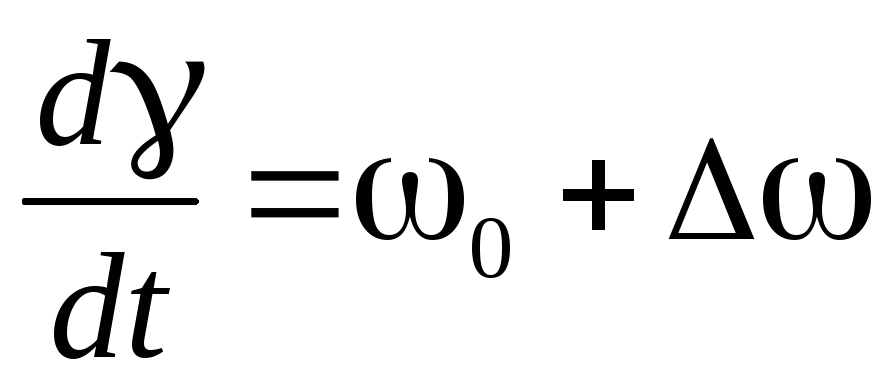 (3.5)
(3.5)
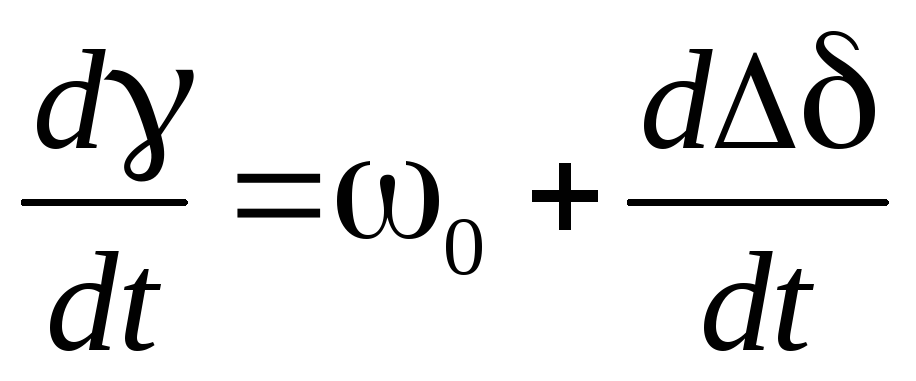 , (3.6)
, (3.6)
то вторая производная
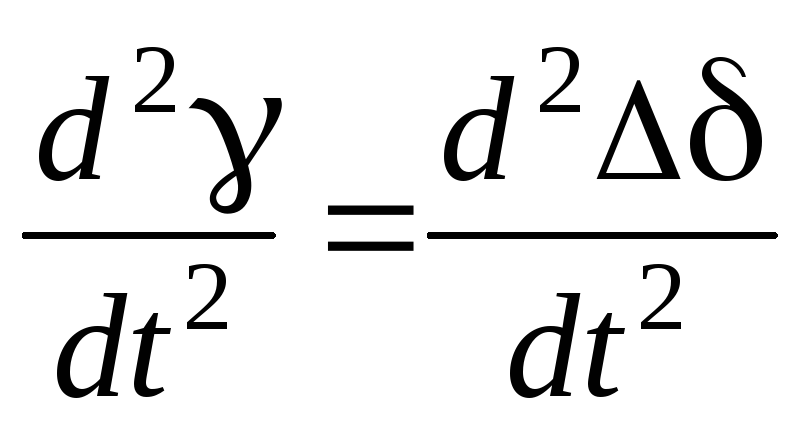 . (3.7)
. (3.7)
Тогда с учетом соотношений (3.6) и (3.7) уравнение (3.3) может быть переписано:
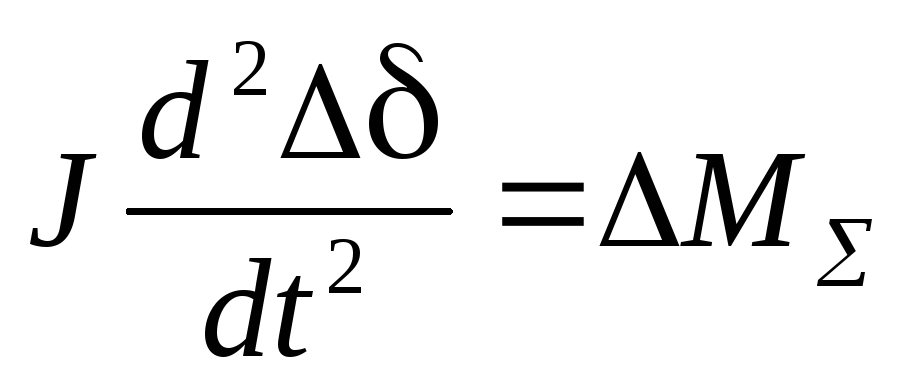 . (3.8)
. (3.8)
Преобразуем (3.8), для чего разделим левую и правую части на отношение  , тогда
, тогда
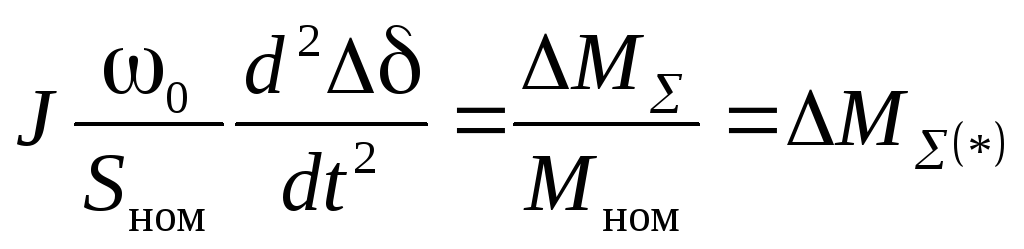 . (3.9)
. (3.9)
Левую часть (3.9) умножим на  и разделим на
и разделим на :
:
 . (3.10)
. (3.10)
Здесь  , где подTJпонимается постоянная инерции ротора генератора, которая имеет размерность времени в секундах. И тогда с учетом этого обозначения (3.10) перепишем:
, где подTJпонимается постоянная инерции ротора генератора, которая имеет размерность времени в секундах. И тогда с учетом этого обозначения (3.10) перепишем:
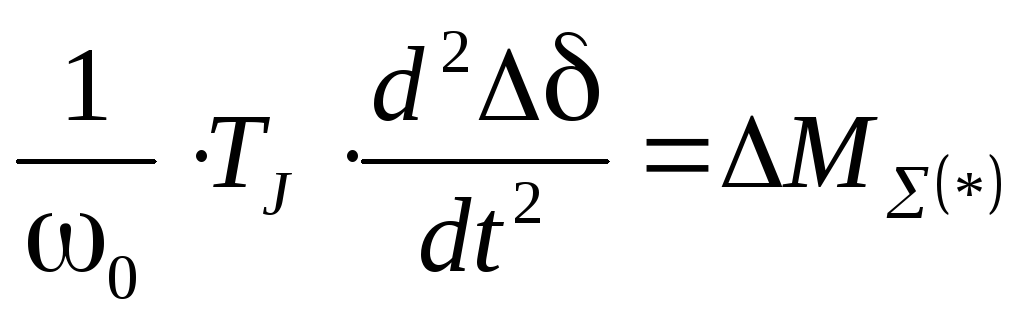 . (3.11)
. (3.11)
Далее перейдем от моментов к мощностям:
 . (3.12)
. (3.12)
Тогда с учетом (3.12) уравнение (3.11) перепишем следующим образом
 . (3.13)
. (3.13)
Это есть не что иное, как полное уравнение движения ротора. Как видно из данного выражения, правая часть уравнения представляет собой безразмерную величину, и поэтому, чтобы получить такую же безразмерную величину в левой части, необходимо подставить в левую часть (3.13): синхронную угловую скорость ωо ,  ; Δδ,
; Δδ, ;t,
;t,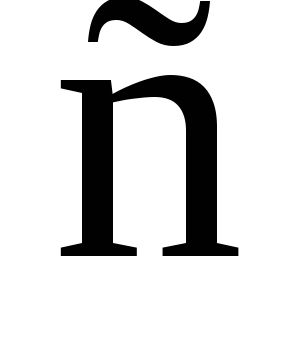 ;ТЈ ,
;ТЈ , . Тогда в левой части также будет получаться безразмерная величина. Можно переписать уравнение (3.13) при применении системы относительных единиц для всех величин, входящих в это уравнение. В такой системе базисными величинами дополнительно принимают угол в один радиан и синхронную угловую скорость ωо. В этом случае единица времени, принимаемая за базисное время (tбаз), будет определяться как промежуток времени в секундах, в течение которого при синхронной угловой скорости вращения ротора ωо будет достигаться изменение угла, равное одному радиану. Тогда
. Тогда в левой части также будет получаться безразмерная величина. Можно переписать уравнение (3.13) при применении системы относительных единиц для всех величин, входящих в это уравнение. В такой системе базисными величинами дополнительно принимают угол в один радиан и синхронную угловую скорость ωо. В этом случае единица времени, принимаемая за базисное время (tбаз), будет определяться как промежуток времени в секундах, в течение которого при синхронной угловой скорости вращения ротора ωо будет достигаться изменение угла, равное одному радиану. Тогда
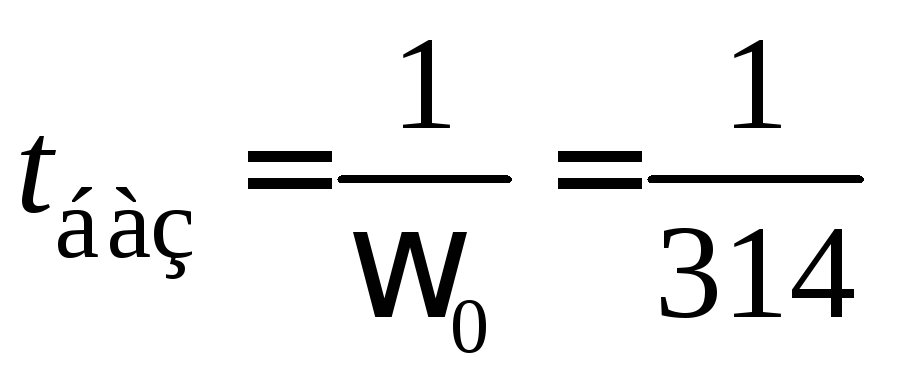 ,
,
где синхронная скорость вращения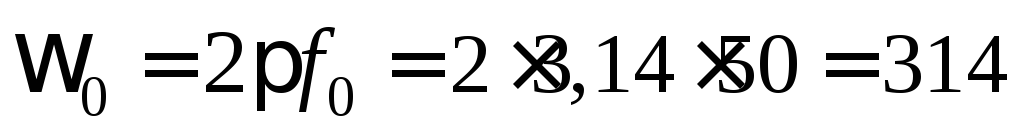 рад/с.
рад/с.
И тогда время, выраженное в относительных единицах или, как иногда говорят, в радианах, будет определяться как
 . (3.14)
. (3.14)
Если применить (3.14) ко времени t и постоянной инерции ТЈ в выражении (3.13), тогда последнее перепишется следующим образом
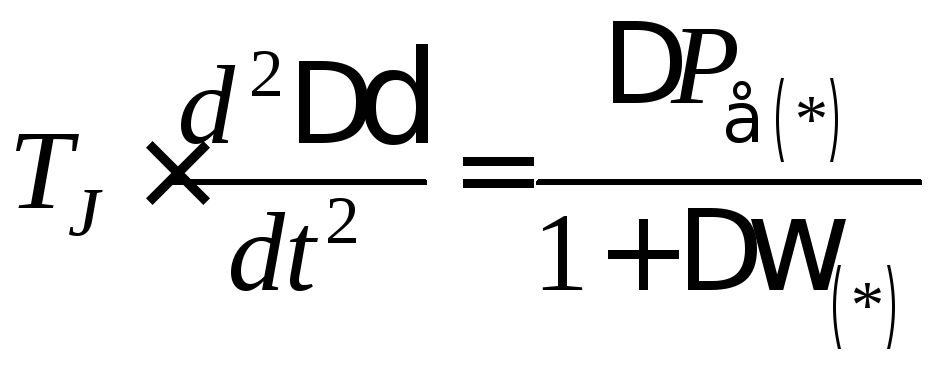 . (3.15)
. (3.15)
Если допустить Δω* = 0, то получим приближенное уравнение движения ротора синхронной машины:
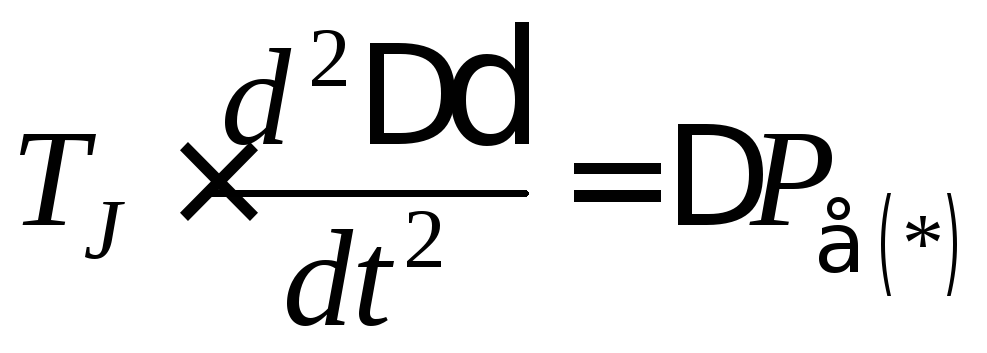 . (3.16)
. (3.16)
Следует отметить, что применение этого приближенного уравнения движения ротора не вносит неприемлемых погрешностей в результат расчета синхронной динамической устойчивости. Это объясняется тем, что в действительности размах синхронных динамических качаний Δδ = (100–120)° при длительности качаний T = (0,5–0,8) с (рис. 3.4).
В этих условиях Δω = 200 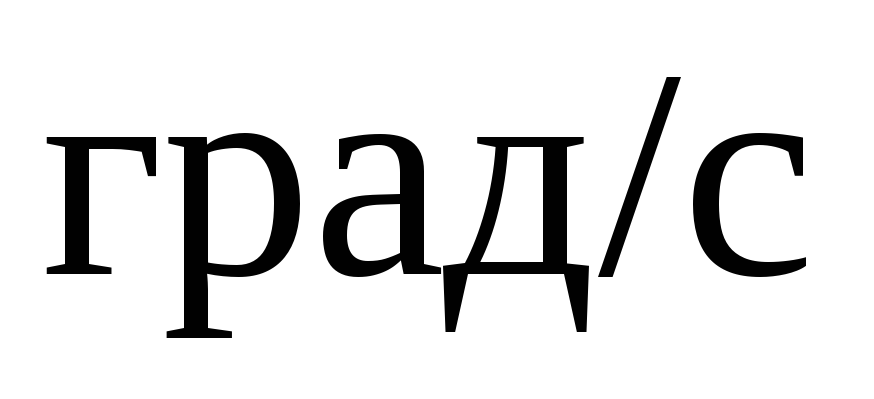 что, отнесенное к ωном, составит
что, отнесенное к ωном, составит
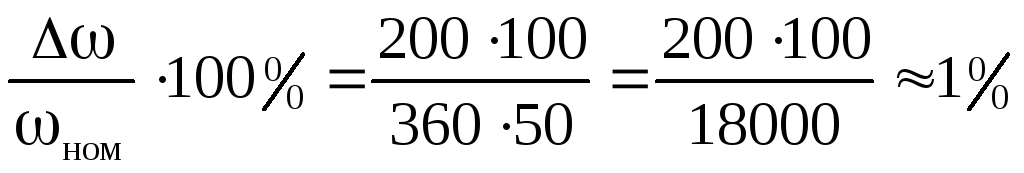 .
.
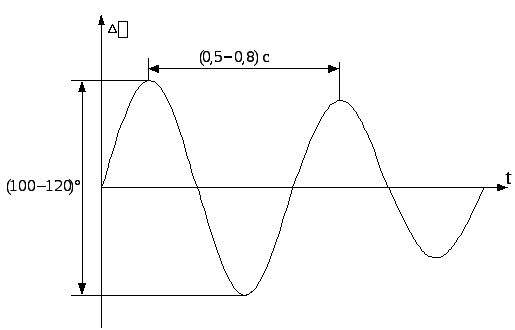
Рис. 3.4. Изменение угла во времени и определение
размаха колебаний и периода качаний
Таким образом, отсюда видно, что скорость перемещения ротора Δω относительно синхронно вращающейся оси, выраженная в относительных единицах, будет немного превышать один процент, что с полным основани-
ем доказывает, что этим можно пренебречь при выполнении приближенных упрощенных расчетов динамической устойчивости. При выполнении же расчетов длительных переходных процессов, таких как синхронизация генераторов, этим допущением Δω = 0 пользоваться не следует, и тогда анализ процесса синхронизации следует проводить по полному уравнению движения ротора синхронной машины, т. е. уравнению (3.13).
Постоянная ТЈ, входящая в уравнение движения ротора, представляет собой физически промежуток времени, в течение которого ротор генератора изменит свою скорость вращения от состояния покоя до синхронной угловой скорости вращения ωо при постоянном вращающем моменте, подведенном к валу ротора генератора, равном номинальному. И наоборот, постоянная инерции ТЈ равна промежутку времени, необходимому для полного останова ротора от синхронной угловой скорости ωо при постоянном тормозящем моменте, подведенном к валу ротора генератора, равном номинальному. Эта постоянная инерции ТЈ в секундах обычно задается в паспортных (каталожных) данных генератора или ее можно определить по эмпирическим формулам следующего вида:
– в паспортных данных задан маховый момент, т. е. GD 2 :
 ,
,
где GD 2 − произведение веса на диаметр ротора, т м 2 ; n – частота вращения ротора, об/мин; Sном − номинальная мощность генератора, МВ·А;
м 2 ; n – частота вращения ротора, об/мин; Sном − номинальная мощность генератора, МВ·А;
– указан момент инерции J, т м 2 :
м 2 :
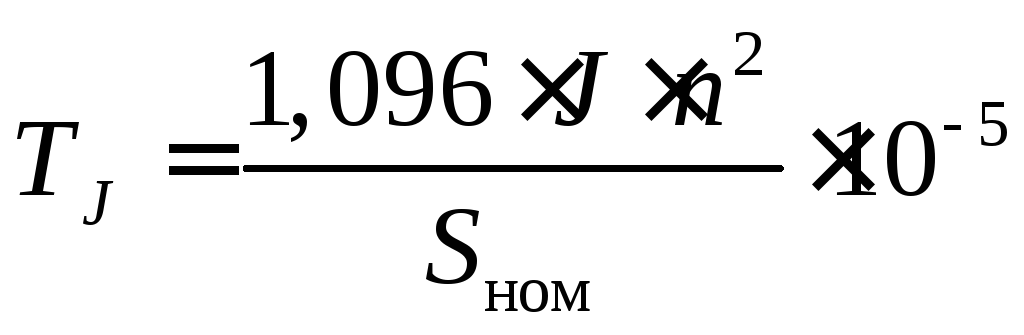 .
.
Для большинства серийно выпускаемых генераторов ТЈ = 5−10 с.
Решение уравнения движения ротора генератора методом последовательных интервалов
Качественную оценку переходного процесса смены режимов выполняют по зависимости δ = f(t),которую получают численным решением уравнения движения ротора генератора  методом последовательных интервалов. При этом можно учесть влияние управляющих воздействий на характер переходного процесса от регулирования возбуждения, изменения времени отключения поврежденного элемента, АПВ и т. д.
методом последовательных интервалов. При этом можно учесть влияние управляющих воздействий на характер переходного процесса от регулирования возбуждения, изменения времени отключения поврежденного элемента, АПВ и т. д.
Переходный процесс, описываемый данным уравнением, разбивают на ряд равных интервалов времени D t.В практических расчетах интервал времени берут в пределах 0,02-0,1 в зависимости от длительности КЗ и характеристик устройств системной автоматики. Переходный процесс рассматривают последовательно по интервалам. В каждом интервале времени избыток мощности (левая часть уравнения) считают неизменным и при этом допущении вычисляют приращение угла D δ.
В момент сброса мощности (момент KЗ) возникает избыток мощности D P0 (рис. 17). Приращение угла в течение первого интервала времени D t находят при начальных условиях  последовательным интегрированием уравнения (1):
последовательным интегрированием уравнения (1):
 ; δ1 =δ0+ ∆δ1. (9.33)
; δ1 =δ0+ ∆δ1. (9.33)
Во втором интервале времени ротор генератора движется под действием избытка мощности D P=Р0 -Р max 2 ∙ sinδ 1 и некоторой начальной скорости, приобретенной в первом интервале:
 . (9.34)
. (9.34)
Решив уравнение переходных процессов относительно приращения угла во втором интервале времени, получим
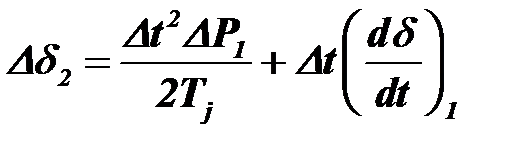 . (9.35)
. (9.35)

Рис. 17 — К расчету динамической устойчивости системы методом последовательных интервалов
После преобразования (9.33) с учетом (9.34) и (9.35) найдем
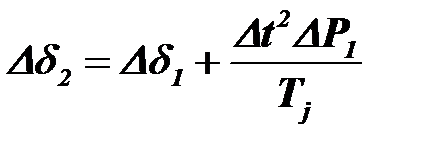 . (9.36)
. (9.36)
Если постоянную инерции TJ и время ∆t выразить в секундах, углы D δ1 и D δ2 — в градусах и ввести постоянную 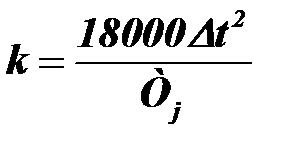 , то выражение (9.36) примет вид
, то выражение (9.36) примет вид
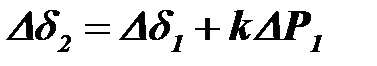 . (9.37)
. (9.37)
Для n-го интервала времени по аналогии запишем
 . (9.38)
. (9.38)
Если в i-м интервале времен и происходит изменение режима с переходом из одной угловой характеристики мощности на другую, то приращение угла определяется выражением
 . (9.39)
. (9.39)
Расчет точек кривой δ = f ‘ ( n ∆t) следует выполнять до тех пор, пока угол δ не начнет уменьшаться по кривой 1 (см. рис. 17), что соответствует сохранению устойчивости, или пока не будет установлено, что угол δ продолжает возрастать по кривой 2, соответствующей нарушению устойчивости. По кривой δ = f(t) можно определить также предельное время отключения КЗ, используя вычисленное по (3.11) значение предельного угла отключения поврежденной цепи ЛЭП.
Пример 1.2. Определить предельное время отключения поврежденной цепи ЛЭП в СЭС, схема которой изображена на рисунке 13 при трехфазном КЗ в начале линии.
Решение. Предельное время отключения трехфазного КЗ можно определить по предельному углу отключения, значение которого найдем по методу площадей. Для этого построим угловые характеристики мощности для нормального и послеаварийного режимов. Для этого построим угловые характеристики мощности для нормального и послеаварийного режимов. В аварийном режиме при трехфазном КЗ мощность, передаваемая в сеть, равна нулю.
Схемы замещения СЭС для нормального и послеаварийного режимов показаны на рисунке 14,бив. Результирующие сопротивления в нормальном режиме
в послеаварийном режиме
Угловые характеристики мощности: в нормальном режиме
 ;
;
в послеаварийном режиме Р.
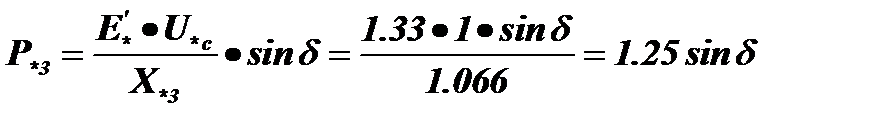 .
.
По характеристике нагрузки и угловым характеристикам мощности находим: угол между 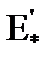 иU*c в нормальном режиме
иU*c в нормальном режиме
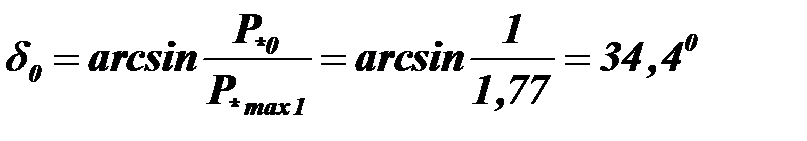 ;
;
критический угол в послеаварийном режиме
 .
.
Предельный угол отключения поврежденной цепи ЛЭП при  .
.
Предельное время отключения трехфазного КЗ
 .
.
Предельное время отключения трехфазного КЗ
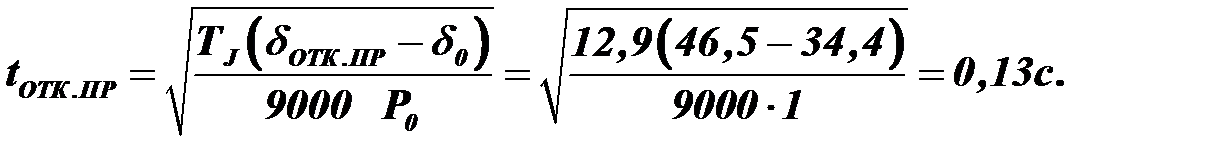
Пример 2.3. Проверить динамическую устойчивость СЭС из предыдущего примера при переходящем двухфазном КЗ на землю в начале одной линии ЛЭП с последующим трехфазным АПВ. Длительность КЗ t=0,2c, продолжительность бестоковой паузы АПВ t АПВ =0,4 c . Параметры элементов системы в аварийном режиме: Х*2г=0,142; X*2тр1=X*0тр1=X*тр1; X*2тр2=X*0тр2=X*тр1; Х*2л=Х*л; Х*0л=2,06.
Решение. Оценим устойчивость СЭС при двухфазном КЗ по характеру изменения угла б во времени. Эту зависимость рассчитаем методом последовательных интервалов.
Угловые характеристики мощности для нормального и послеаварийного режимов рассчитаны в примере 1. Определим угловую характеристику мощности системы в аварийном режиме.
Схема замещения СЭС для этого режима показана на рисунке 15,в, где дополнительное сопротивление, обусловленное несимметрией, определяется через результирующее сопротивление обратной последовательности:
 ;
;
и результирующее сопротивление нулевой последовательности
 .
.
Так как  , то взаимное сопротивление между рассматриваемыми точками системы в аварийном режиме
, то взаимное сопротивление между рассматриваемыми точками системы в аварийном режиме
 .
.
Уравнение угловой характеристики мощности
 .
.
Рассчитаем зависимость δ = f(t) , приняв длительность интервала Δ t =0,1 c, при котором постоянная
K =18000( Δt ) 2 / Tj =18000-0,1 2 /12,9=14.
Первый интервал. Угол δ0 в момент возникновения КЗ остается неизменным, а мощность снижается до значения
P(0)=Pmax2 Sin δ 0 =0,5 · sin34,4°=0,282.
Избыток мощности в начале первого интервала
Приращение угла δ1, в течение первого интервала
Угол δ1 в конце первого интервала
Второй интервал.
Мощность генератора в конце первого интервала
P*1=Pmax2 Sin δ 1 = 0,5 sin39,4°=0,318 .
Избыток мощности в начале второго интервала
Приращение угла Δδ2 в течение второго интервала
Угол δ2 в конце второго интервала
Третий интервал. В начале третьего интервала происходит отключение поврежденной цепи ЛЭП. Мощность генератора и избыток мощности до отключения поврежденной цепи
Мощность генератора и избыток мощность после отключения поврежденной
Приращение угла Δδ3 в третьем интервале
Угол δ3 в конце третьего интервала
Расчет четвертого и пятого интервалов выполняем так же, как и расчет второго интервала, только мощность генератора уже вычисляется по угловой характеристике мощности послеаварийного режима.
В начале шестого интервала (при t = tK З + tA ПВ =0,2+0,4=0,6 c ) срабатывает устройство АПВ. Расчет шестого интервала выполняем аналогично расчету третьего интервала, только используем угловые характеристики мощности послеаварийного и нормального режимов.
Последующие интервалы рассчитываем аналогично расчету второго интервала, только используем угловую характеристику мощности нормального режима.
Результаты расчетов сведены в таблицу 9.6.
Полученные данные свидетельствуют о том, что динамическая устойчивость СЭС при двухфазном КЗ на землю с последующим трехфазным АПВ сохраняется. Без АПВ система не сохранила бы устойчивость, так как предельный угол отключения двухфазного КЗ на землю
 ,
,
а при фактической длительности КЗ t кз =0,2с угол отключения КЗ больше и равен 53,9° (см.таблицу 9.6).
Таблица 9.6 — Результаты расчетов динамической устойчивости
| t,c | 5, град | Р. | ДР. | Д8,град | Примечание |
| 0 | 34,4 | 0,282 | 0,718 | 5 | Расчет по Р*2 (5) |
| 0,1 | 39,4 | 0,318 | 0,682 | 14,5 | То же |
| 0,2 | 53,9 | 0,404 | 0,596 | 18,5 | Переход с Р*2 (8) |
| 1,01 | -0,01 | на Р*3 (5) | |||
| 0,3 | 72,4 | 1,19 | -0,19 | 15,8 | Расчет по Р*3 (5) |
| 0,4 | 88,2 | 1,25 | -0,25 | 12,3 | То же |
| 0,5 | 100,5 | 1,23 | -0,23 | 9,1 | То же |
| 0,6 | 109,1 | 1,18 | -0,18 | 3,1 | Переход с P*3 (S) |
| 1,67 | -0,67 | на Р*1(5) | |||
| 0,7 | 112,2 | 1,64 | -0,64 | -5,9 | Расчет по Р*1(5) |
| 0,8 | 106,3 | — | — | — | То же |
ПРИЛОЖЕНИЕ А
Дата добавления: 2020-04-08 ; просмотров: 179 ; Мы поможем в написании вашей работы!