Что такое поток сцепление
Потокосцепление и магнитный поток
Из опыта известно, что возле постоянных магнитов, равно как и вблизи проводников с током, можно наблюдать физические эффекты, такие как механическое действие на другие магниты или проводники с током, а также появление ЭДС в движущихся в данном пространстве проводниках.
Необычное состояние пространства возле магнитов и проводников с током, называется магнитным полем, количественные характеристики которого легко определяются по данным явлениям: по силе механического воздействия или по электромагнитной индукции, по сути — по величине наводимой в движущемся проводнике ЭДС.

Явление наведения ЭДС в проводнике (явление электромагнитной индукции) проявляет себя в различных условиях. Вы можете двигать проводник через однородное магнитное поле, а можете просто изменять магнитное поле возле неподвижного проводника. В обоих случаях изменяющееся в пространстве магнитное поле станет наводить в проводнике ЭДС.
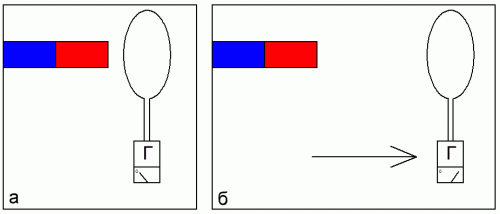
Простое экспериментальное приспособление для исследования данного явления изображено на рисунке. Здесь проводящее (медное) кольцо соединено своими выводами с баллистическим гальванометром, по отклонению стрелки которого можно будет судить о количестве электрического заряда, проходящего через эту нехитрую цепь. Сначала разместим кольцо центром в какой-нибудь точке пространства около магнита (положение а), затем резко отодвинем кольцо (в положение б). Гальванометр покажет значение прошедшего по цепи заряда Q.
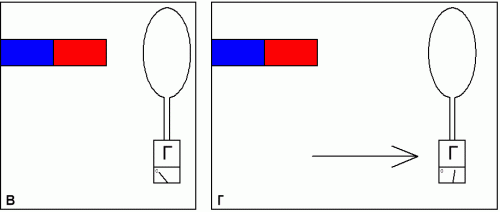
Теперь поместим кольцо в другую точку, чуть-чуть подальше от магнита (в положение в), и снова, с такой же скоростью, резко отодвинем его в сторону (в положение г). Отклонение стрелки гальванометра будут меньше чем в первом эксперименте. А если увеличить сопротивление петли R, например заменив медь на вольфрам, то перемещая кольцо аналогичным образом мы заметим, что гальванометр покажет заряд еще меньший, однако величина этого движущегося через гальванометр заряда в любом случае будет обратно пропорциональна сопротивлению петли.
Эксперимент отчетливо демонстрирует, что пространство вокруг магнита в каждой его точке обладает каким-то свойством, чем-то таким, что напрямую влияет на количество заряда, проходящего через гальванометр, когда мы отодвигаем кольцо от магнита. Назовем это что-то, находящееся около магнита, магнитным потоком, и обозначим его количественную величину буквой Ф. Отметим выявленную зависимость Ф
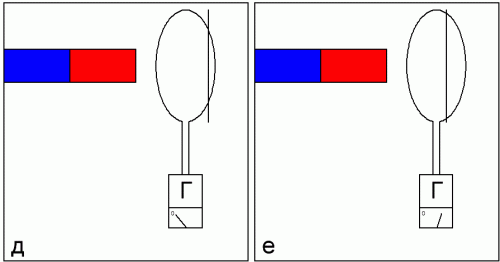
Усложним эксперимент. Закрепим медную петлю в определенной точке напротив магнита, рядом с ним (в положении д), но теперь будем изменять площадь петли (перекрывая ее часть проводником). Показания гальванометра будут пропорциональны изменению площади кольца (в положении е).
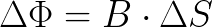
Следовательно действующий на петлю магнитный поток Ф от нашего магнита пропорционален площади петли. А вот магнитная индукция B, связанная с положением кольца относительно магнита, но не зависящая от параметров кольца, определяет свойство магнитного поля в каждой рассматриваемой точке пространства возле магнита.
Продолжая эксперименты с медным кольцом, теперь будем изменять положение плоскости кольца относительно магнита в начальный момент (положение ж), и затем поворачивать его до положения вдоль оси магнита (положение з).
Заметим, что чем больше изменение угла между кольцом и магнитом — тем больше заряда Q протекает по цепи через гальванометр. Это значит, что магнитный поток через кольцо пропорционален косинусу угла между магнитом и нормалью к плоскости кольца.
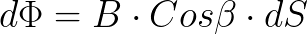
Таким образом можно заключить, что магнитная индукция B – есть величина векторная, направление которой в данной точке совпадает с направлением нормали к плоскости кольца в том его положении, когда при резком отодвигании кольца далеко от магнита, проходящий по цепи заряд Q максимален.
Вместо магнита в эксперименте можно применять катушку электромагнита, отодвигать эту катушку или изменять в ней ток, усиливая или уменьшая таким образом магнитное поле, пронизывающее экспериментальный виток.
Площадь, пронизываемая магнитным полем, не обязательно может быть ограничена круглым витком, это может быть в принципе любая поверхность, магнитный поток через которую определяется тогда путем интегрирования:
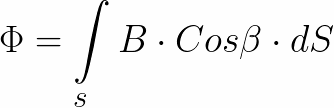
Выходит, что магнитный поток Ф — это поток вектора магнитной индукции B через поверхность S. А магнитная индукция B – это плотность магнитного потока Ф в данной точке поля. Магнитный поток Ф измеряется в единицах «Вебер» — Вб. Магнитная индукция B измеряется в единицах «Тесла» — Тл.
Если все пространство вокруг постоянного магнита или катушки с током исследовать подобным образом, при помощи витка с гальванометром, то можно построить в этом пространстве бесчисленное множество так называемых «магнитных линий» — линий вектора магнитной индукции B — направление касательных в каждой точке которых будет соответствовать направлению вектора магнитной индукции B в данных точках исследуемого пространства.
Разделив пространство магнитного поля воображаемыми трубками единичного поперечного сечения S=1, можно получить так называемые единичные магнитные трубки, оси которых называют единичными магнитными линиями. При помощи данного подхода можно наглядно изобразить количественную картину магнитного поля, и в этом случае магнитный поток будет равен количеству линий, проходящих через выбранную поверхность.
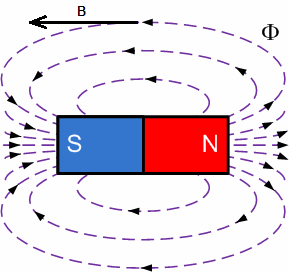
Магнитные линии непрерывны, они выходят из северного полюса и обязательно входят в южный, поэтому суммарный магнитный поток через любую замкнутую поверхность равен нулю. Математически это выглядит так:
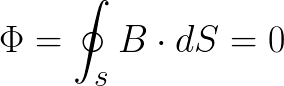
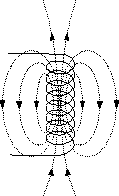
Рассмотрим магнитное поле, ограниченное поверхностью цилиндрической катушки. По сути — магнитный поток, пронизывающий поверхность, образованную витками данной катушки. В этом случае общую поверхность можно разделить на отдельные поверхности для каждого из витков катушки. На рисунке видно, что поверхности верхних и нижних витков катушки пронизываются четырьмя единичными магнитными линиями, а поверхности витков в середине катушки — восемью.
Чтобы найти величину полного магнитного потока через все витки катушки, необходимо суммировать магнитные потоки, пронизывающие поверхности каждого из ее витков, то есть магнитные потоки, сцепленные с отдельными витками катушки:
Ф = Ф1+Ф2+Ф3+Ф4+Ф5+Ф6+Ф7+Ф8, если в катушке 8 витков.
Для примера симметричной катушки, изображенной на предыдущем рисунке:
Ф верхних витков = 4+4+6+8 = 22;
Ф нижних витков = 4+4+6+8 = 22.
Ф общее = Ф верхних витков + Ф нижних витков = 44.
Здесь и вводится понятие «потокосцепление». Потокосцепление — это общий магнитный поток, сцепленный со всеми витками катушки, численно равный сумме магнитных потоков, сцепленных с отдельными ее витками:
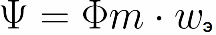
Фm — магнитный поток, создаваемый током через один виток катушки; wэ — эффективное число витков в катушке;
Потокосцепление — величина виртуальная, так как реально нет никакой суммы отдельных магнитных потоков, а есть общий магнитный поток. Тем не менее, когда реальное распределение магнитного потока по виткам катушки неизвестно, а известно потокосцепление, то катушку можно заменить эквивалентной, вычислив количество эквивалентных одинаковых витков, необходимых для получения требуемого общего магнитного потока.
Если Вам понравилась эта статья, поделитесь ссылкой на неё в социальных сетях. Это сильно поможет развитию нашего сайта!
Подписывайтесь на наш канал в Telegram!
Просто пройдите по ссылке и подключитесь к каналу.
Не пропустите обновления, подпишитесь на наши соцсети:
Потокосцепление
Потокосцепле́ние (полный магнитный поток) — физическая величина, представляющая собой суммарный магнитный поток, сцепляющийся со всеми витками катушки индуктивности.
Содержание
Определение
Потокосцепление численно равно сумме магнитных потоков, проходящих через каждый виток катушки, т.е. при количестве витков N и одинаковом магнитном потоке в каждом витке потокосцепление можно определить как  где
где  — магнитный поток одного витка [ Вб ].
— магнитный поток одного витка [ Вб ].
В идеальном соленоиде все магнитные силовые линии проходят через каждый виток (т.е. не пересекают боковую поверхность соленоида), и, следовательно, магнитный поток каждого витка одинаков. Однако на практике магнитные потоки в витках катушки отличаются и величина потокосцепления определяется по формуле:

где:
 — количество витков;
— количество витков;
 — номер витка, с которым сцеплен поток
— номер витка, с которым сцеплен поток 
В случае, если катушка имеет ферромагнитный сердечник, потокосцепление можно определить по формуле:

где  — магнитный поток через магнитопровод (сердечник) катушки.
— магнитный поток через магнитопровод (сердечник) катушки.
Величина потокосцепления, помимо магнитного потока, имеет связь с током I в индуктивности, определяющуюся выражением:

где  — индуктивность катушки [ Гн ].
— индуктивность катушки [ Гн ].
Эта формула выражает принцип непрерывности во времени потокосцепления катушки индуктивности.
Принцип непрерывности
Запас энергии магнитного поля в катушке индуктивности не может измениться скачком. Это выражает принцип непрерывности во времени. Невозможность скачкообразного изменения потокосцепления индуктивности объясняется, в свою очередь, тем, что в противном случае на индуктивности появилось бы бесконечно большое напряжение, что противоречит опыту.
Принцип непрерывности также означает, что ток в индуктивности не может измениться скачком (см. переходные процессы в электрических цепях):
 — первый закон коммутации.
— первый закон коммутации.
См. также
- Магнитный поток
- Индуктивность
- Катушка индуктивности
Литература
- Иродов И.Е. Электромагнетизм. Основные законы. 2010. 319 с. — ISBN 978-5-9963-0281-9
Wikimedia Foundation . 2010 .
- Потолок (авиация)
- Потомок Чингисхана (фильм)
Полезное
Смотреть что такое «Потокосцепление» в других словарях:
потокосцепление — потокосцепление … Орфографический словарь-справочник
ПОТОКОСЦЕПЛЕНИЕ — полный магнитный поток, пронизывающий электрический контур. Напр., потокосцепление многовитковой катушки индуктивности равно сумме потоков через все ее витки. Единица измерения Вб … Большой Энциклопедический словарь
потокосцепление — сущ., кол во синонимов: 1 • поток (55) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Потокосцепление — сумма магнитных потоков, сцепленных с элементами контура электрической цепи. Источник: ЭЛЕКТРОТЕХНИКА . ТЕРМИНЫ И ОПРЕДЕЛЕНИЯ ОСНОВНЫХ ПОНЯТИЙ. ГОСТ Р 52002 2003 (утв. Постановлением Госстандарта РФ от 09.01.2003 N 3 ст) … Официальная терминология
потокосцепление — Сумма магнитных потоков, сцепленных с элементами контура электрической цепи. [ГОСТ Р 52002 2003] Тематики электротехника, основные понятия … Справочник технического переводчика
потокосцепление — 113 потокосцепление Сумма магнитных потоков, сцепленных с элементами контура электрической цепи 114 потокосцепление самоиндукции Потокосцепление элемента электрической цепи, обусловленное электрическим током в этом элементе 115 (собственная)… … Словарь-справочник терминов нормативно-технической документации
потокосцепление — полный магнитный поток, пронизывающий электрический контур. Например, потокосцепление многовитковой катушки индуктивности равно сумме потоков через все её витки. Единица измерения вебер (Вб). * * * ПОТОКОСЦЕПЛЕНИЕ ПОТОКОСЦЕПЛЕНИЕ, полный… … Энциклопедический словарь
Потокосцепление — в электротехнике, полный магнитный поток (ψ), сцепленный с рассматриваемым контуром. По существу П. всегда совпадает с потоком в интегральном определении: Φ = = ψ, где В вектор магнитной индукции, рис.); при этом общий поток, или П., ω… … Большая советская энциклопедия
потокосцепление — visuminė magnetovara statusas T sritis Standartizacija ir metrologija apibrėžtis Visuminis elektrinio laidumo srovės, tekančios uždaruoju kontūru, stipris. atitikmenys: angl. current linkage vok. Flussverkettung, f rus. потокосцепление, n pranc.… … Penkiakalbis aiškinamasis metrologijos terminų žodynas
потокосцепление — visuminė magnetovara statusas T sritis fizika atitikmenys: angl. current linkage vok. Flussverkettung, f rus. потокосцепление, n pranc. flux embrassé, m; flux magnétique embrassé, m … Fizikos terminų žodynas
Магнитный поток и потокосцепление
В пространстве, окружающем проводники, по которым протекает электрический ток, а также окружающем постоянные магниты, существует ряд физических явлений, проявляющихся в возникновении ЭДС в движущихся проводниках, механическом воздействии на постоянные магниты и проводники с током, находящиеся в этом пространстве и др.
Особое состояние физического пространства, в котором происходят эти явления, называется магнитным полем .
Для определения количественных характеристик магнитного поля можно использовать любое его проявление, однако обычно используют явление электромагнитной индукции и механическое воздействие со стороны поля.
Явление электромагнитной индукции заключается в возникновении ЭДС проводниках . Причем, условия, при которых она возникает могут быть самыми различными. Это может происходить, например, при движении проводника в однородном магнитном поле или в неподвижном проводнике, находящемся в переменном магнитном поле.

Определить основные соотношения для этого явлении можно с помощью устройства показанного на рис. 1. Оно представляет собой тонкий проводник, изогнутый в виде кольца K и подключенный гибким витым проводом к баллистическому гальванометру G . Отклонение стрелки баллистического гальванометра пропорционально количеству зарядов q , протекших через него.
Если центр кольца K помещать в разные точки пространства вокруг постоянного магнита, а затем быстро относить на значительное расстояние, то гальванометр будет фиксировать разные значения q . Расстояние, на которое нужно удалять кольцо теоретически должно быть бесконечным для того, чтобы все проявления поля были сведены к нулю.
При повторении опыта из одной и той же точки пространства мы будем получать одинаковые значения q , но если изменить сопротивление цепи r , по которой протекают заряды, то величина q изменится обратно пропорционально r . Отсюда можно сделать заключение, что каждая точка пространства вокруг постоянного магнита обладает некоторым свойством, определяющим количество зарядов q , протекающих через гальванометр при удалении кольца K на значительное расстояние от магнита. Обозначим это свойство символом Ф и назовем его магнитным потоком , оставляя пока смысловое обоснование термина. Тогда можно записать отмеченную выше связь в виде выражения:
q = Ф/ r или Ф = qr
Повторим опыты с кольцом в одной и той же точке пространства постоянного магнита, например, в точке a рис. 1, при неизменном сопротивлении цепи и положении плоскости кольца. При этом будем постепенно изменять площадь кольца. Если площадь кольца достаточно малая, то изменения количества зарядов Δ q будут в точности пропорциональны изменению площади кольца Δ s . Но количество зарядов пропорционально величине магнитного потока, поэтому и изменения магнитного потока пропорциональны изменению площади, т.е.
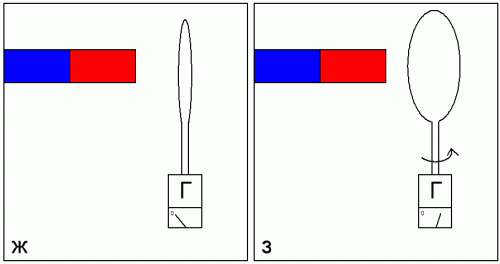
Δ Ф = B a Δ s или, переходя к бесконечно малым, d Ф = B a ds ,
где величина B a не зависит от размеров кольца и определяется только положением точки a , следовательно, она характеризует магнитное поле в данной точке пространства и называется магнитной индукцией .
Если опыты в точке a продолжить, изменяя положение плоскости кольца в начальный момент, то можно установить, что существует такое его положение, при котором количество зарядов будет максимальным и всякое отклонение от этого положения будет приводить к их уменьшению пропорционально косинусу угла отклонения. Включая это условие в выражение (2) получим
d Ф = B a cosβ ds ,
где β — угол между направлением нормали к плоскости пробного витка и направлением, при котором количество зарядов, протекающих через виток максимально.
Выражение (3) показывает, что магнитная индукция B является векторной величиной и ее направление совпадает с направлением нормали к плоскости пробного витка, при котором количество зарядов, протекающих через виток при его удалении на значительное расстояние, максимально.
Опыты с пробным витком (кольцом) можно проводить также и в пространстве катушки, подключенной к источнику постоянного тока. При этом вместо удаления витка можно просто выключать ток, т.к. в обоих случаях магнитный поток будет уменьшаться до нуля.

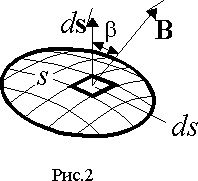
Если в пространстве выделить некоторую поверхность s , то магнитный поток через эту поверхность определится из выражения (3) в виде

где d s — вектор численно равный поверхности ds и имеющий направление нормали к этой поверхности (рис 2.).
Из выражения (4) следует, что:
Если поверхность ds нормальна к вектору B , то cosβ = 1 и из выражения (3)

Возвращаясь к полученному ранее выражению (1), можно количественно определить магнитный поток через некоторую поверхность как произведение величины заряда, протекающего через проводник совмещенный с границей этой поверхности при полном исчезновении магнитного поля, на сопротивление электрической цепи, по которой протекают эти заряды .
В описанных выше опытах с пробным витком (кольцом), он удалялся на такое расстояние, при котором исчезали всякие проявления магнитного поля. Но можно просто перемещать этот виток в пределах поля и при этом в нем также будут перемещаться электрические заряды. Перейдем в выражении (1) к приращениям
Ф + Δ Ф = r ( q — Δ q ) => Δ Ф = — rΔ q => Δ q = -Δ Ф/ r
где Δ Ф и Δ q — приращения потока и количества зарядов. Разные знаки приращений объясняются тем, что положительный заряд в опытах с удалением витка соответствовал исчезновению поля, т.е. отрицательному приращению магнитного потока.
С помощью пробного витка можно исследовать все пространство вокруг магнита или катушки с током и построить линии, направление касательных к которым в каждой точке будет соответствовать направлению вектора магнитной индукции B (рис. 3)

Эти линии называются линиями вектора магнитной индукции или магнитными линиями .
Пространство магнитного поля можно мысленно разделить трубчатыми поверхностями, образованными магнитными линиями, причем, поверхности можно выбрать таким образом, чтобы магнитный поток внутри каждой такой поверхности (трубки) численно был равен единице и изобразить графически осевые линии этих трубок. Такие трубки называют единичными, а линии их осей — единичными магнитными линиями . Картина магнитного поля изображенная с помощью единичных линий дает не только о качественное, но и количественное представление о нем, т.к. при этом величина вектора магнитной индукции оказывается равной количеству линий, проходящих через единицу поверхности, нормальной вектору B , а количество линий, проходящих через любую поверхность равно значению магнитного потока .
Магнитные линии непрерывны и этот принцип можно математически представить в виде

т.е. магнитный поток, проходящий через любую замкнутую поверхность равен нулю .

Выражение (4) справедливо для поверхности s любой формы. Если рассматривать магнитный поток проходящий через поверхность, образованную витками цилиндрической катушки (рис. 4), то ее можно разделить на поверхности, образованные отдельными витками, т.е. s = s 1 + s 2 +. + s 8 . Причем через поверхности разных витков в общем случае будут проходить разные магнитные потоки. Так на рис. 4, через поверхности центральных витков катушки проходят восемь единичных магнитных линий, а через поверхности крайних витков только четыре.
Для того, чтобы определить полный магнитный поток, проходящий через поверхность всех витков, нужно сложить потоки, проходящие через поверхности отдельных витков, или, иначе говоря, сцепляющиеся с отдельными витками. Например, магнитные потоки, сцепляющиеся с четырьмя верхними витками катушки рис. 4, будут равны: Ф 1 =4; Ф 2 =4; Ф 3 =6; Ф 4 =8. Также, зеркально-симметрично с нижними.
То есть для приведенного на рисунке случая, двух зеркально-симметричных половинок катушки:
Ψ = 2(Ф 1 + Ф 2 + Ф 3 + Ф 4 ) = 48
Виртуальность, то есть воображаемость потокосцепления проявляется в том, что оно не представляет собой реального магнитного потока, который никакая индуктивность не может кратно увеличивать, но поведение импеданса катушки таково, что кажется, что магнитный поток увеличивается кратно эффективному количеству витков, хотя реально — это просто взаимодействие витков в том же самом поле. Если бы катушка увеличивала магнитный поток своим потокосцеплением, то можно было бы создавать умножители магнитного поля на катушке даже без тока, ибо потокосцепление не подразумевает замкнутости цепи катушки, но лишь совместную геометрию близости витков.
Часто реальное распределение потокосцепления по виткам катушки неизвестно, но его можно принять равномерным и одинаковым для всех витков, если реальную катушку заменить эквивалентной с другим числом витков w э , сохраняя при этом величину потокосцепления Ψ = w э Ф m , где Ф m — поток, сцепляющийся с внутренними витками катушки, а w э — эквивалентное или эффективное число витков катушки. Для рассмотренного на рис. 4 случая w э = Ψ/Ф 4 =48/8=6.
Можно также произвести замену реальной катушки на эквивалентную с сохранением числа витков Ψ = w Ф n . Тогда для сохранения потокосцепления необходимо принять, что со всеми витками катушки сцепляется магнитный поток Ф n = Ψ/ w .
Первый вариант замены катушки эквивалентной сохраняет картину магнитного поля, изменяя параметры катушки, второй — сохраняет параметры катушки, изменяя картину магнитного поля.
Магнитный поток и потокосцепление
В пространстве, окружающем проводники, по которым протекает электрический ток, а также окружающем постоянные магниты, существует ряд физических явлений, проявляющихся в возникновении ЭДС в движущихся проводниках, механическом воздействии на постоянные магниты и проводники с током, находящиеся в этом пространстве и др.
Особое состояние физического пространства, в котором происходят эти явления, называется магнитным полем .
Для определения количественных характеристик магнитного поля можно использовать любое его проявление, однако обычно используют явление электромагнитной индукции и механическое воздействие со стороны поля.
Явление электромагнитной индукции заключается в возникновении ЭДС проводниках . Причем, условия, при которых она возникает могут быть самыми различными. Это может происходить, например, при движении проводника в однородном магнитном поле или в неподвижном проводнике, находящемся в переменном магнитном поле.

Определить основные соотношения для этого явлении можно с помощью устройства показанного на рис. 1. Оно представляет собой тонкий проводник, изогнутый в виде кольца K и подключенный гибким витым проводом к баллистическому гальванометру G . Отклонение стрелки баллистического гальванометра пропорционально количеству зарядов q , протекших через него.
Если центр кольца K помещать в разные точки пространства вокруг постоянного магнита, а затем быстро относить на значительное расстояние, то гальванометр будет фиксировать разные значения q . Расстояние, на которое нужно удалять кольцо теоретически должно быть бесконечным для того, чтобы все проявления поля были сведены к нулю.
При повторении опыта из одной и той же точки пространства мы будем получать одинаковые значения q , но если изменить сопротивление цепи r , по которой протекают заряды, то величина q изменится обратно пропорционально r . Отсюда можно сделать заключение, что каждая точка пространства вокруг постоянного магнита обладает некоторым свойством, определяющим количество зарядов q , протекающих через гальванометр при удалении кольца K на значительное расстояние от магнита. Обозначим это свойство символом Ф и назовем его магнитным потоком , оставляя пока смысловое обоснование термина. Тогда можно записать отмеченную выше связь в виде выражения:
q = Ф/ r или Ф = qr
Повторим опыты с кольцом в одной и той же точке пространства постоянного магнита, например, в точке a рис. 1, при неизменном сопротивлении цепи и положении плоскости кольца. При этом будем постепенно изменять площадь кольца. Если площадь кольца достаточно малая, то изменения количества зарядов Δ q будут в точности пропорциональны изменению площади кольца Δ s . Но количество зарядов пропорционально величине магнитного потока, поэтому и изменения магнитного потока пропорциональны изменению площади, т.е.
Δ Ф = B a Δ s или, переходя к бесконечно малым, d Ф = B a ds ,
где величина B a не зависит от размеров кольца и определяется только положением точки a , следовательно, она характеризует магнитное поле в данной точке пространства и называется магнитной индукцией .
Если опыты в точке a продолжить, изменяя положение плоскости кольца в начальный момент, то можно установить, что существует такое его положение, при котором количество зарядов будет максимальным и всякое отклонение от этого положения будет приводить к их уменьшению пропорционально косинусу угла отклонения. Включая это условие в выражение (2) получим
d Ф = B a cosβ ds ,
где β — угол между направлением нормали к плоскости пробного витка и направлением, при котором количество зарядов, протекающих через виток максимально.
Выражение (3) показывает, что магнитная индукция B является векторной величиной и ее направление совпадает с направлением нормали к плоскости пробного витка, при котором количество зарядов, протекающих через виток при его удалении на значительное расстояние, максимально.
Опыты с пробным витком (кольцом) можно проводить также и в пространстве катушки, подключенной к источнику постоянного тока. При этом вместо удаления витка можно просто выключать ток, т.к. в обоих случаях магнитный поток будет уменьшаться до нуля.
Если в пространстве выделить некоторую поверхность s , то магнитный поток через эту поверхность определится из выражения (3) в виде
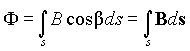
где d s — вектор численно равный поверхности ds и имеющий направление нормали к этой поверхности (рис 2.).
Из выражения (4) следует, что:
Если поверхность ds нормальна к вектору B , то cosβ = 1 и из выражения (3)
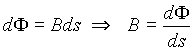
Возвращаясь к полученному ранее выражению (1), можно количественно определить магнитный поток через некоторую поверхность как произведение величины заряда, протекающего через проводник совмещенный с границей этой поверхности при полном исчезновении магнитного поля, на сопротивление электрической цепи, по которой протекают эти заряды .
В описанных выше опытах с пробным витком (кольцом), он удалялся на такое расстояние, при котором исчезали всякие проявления магнитного поля. Но можно просто перемещать этот виток в пределах поля и при этом в нем также будут перемещаться электрические заряды. Перейдем в выражении (1) к приращениям
Ф + Δ Ф = r ( q — Δ q ) => Δ Ф = — rΔ q => Δ q = -Δ Ф/ r
где Δ Ф и Δ q — приращения потока и количества зарядов. Разные знаки приращений объясняются тем, что положительный заряд в опытах с удалением витка соответствовал исчезновению поля, т.е. отрицательному приращению магнитного потока.
С помощью пробного витка можно исследовать все пространство вокруг магнита или катушки с током и построить линии, направление касательных к которым в каждой точке будет соответствовать направлению вектора магнитной индукции B (рис. 3)
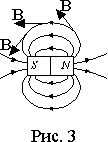
Эти линии называются линиями вектора магнитной индукции или магнитными линиями .
Пространство магнитного поля можно мысленно разделить трубчатыми поверхностями, образованными магнитными линиями, причем, поверхности можно выбрать таким образом, чтобы магнитный поток внутри каждой такой поверхности (трубки) численно был равен единице и изобразить графически осевые линии этих трубок. Такие трубки называют единичными, а линии их осей — единичными магнитными линиями . Картина магнитного поля изображенная с помощью единичных линий дает не только о качественное, но и количественное представление о нем, т.к. при этом величина вектора магнитной индукции оказывается равной количеству линий, проходящих через единицу поверхности, нормальной вектору B , а количество линий, проходящих через любую поверхность равно значению магнитного потока .
Магнитные линии непрерывны и этот принцип можно математически представить в виде
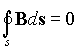
т.е. магнитный поток, проходящий через любую замкнутую поверхность равен нулю .
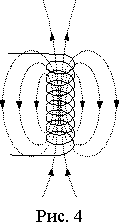
Выражение (4) справедливо для поверхности s любой формы. Если рассматривать магнитный поток проходящий через поверхность, образованную витками цилиндрической катушки (рис. 4), то ее можно разделить на поверхности, образованные отдельными витками, т.е. s = s 1 + s 2 +. + s 8 . Причем через поверхности разных витков в общем случае будут проходить разные магнитные потоки. Так на рис. 4, через поверхности центральных витков катушки проходят восемь единичных магнитных линий, а через поверхности крайних витков только четыре.
Для того, чтобы определить полный магнитный поток, проходящий через поверхность всех витков, нужно сложить потоки, проходящие через поверхности отдельных витков, или, иначе говоря, сцепляющиеся с отдельными витками. Например, магнитные потоки, сцепляющиеся с четырьмя верхними витками катушки рис. 4, будут равны: Ф 1 =4; Ф 2 =4; Ф 3 =6; Ф 4 =8. Также, зеркально-симметрично с нижними.
То есть для приведенного на рисунке случая, двух зеркально-симметричных половинок катушки:
Ψ = 2(Ф 1 + Ф 2 + Ф 3 + Ф 4 ) = 48
Виртуальность, то есть воображаемость потокосцепления проявляется в том, что оно не представляет собой реального магнитного потока, который никакая индуктивность не может кратно увеличивать, но поведение импеданса катушки таково, что кажется, что магнитный поток увеличивается кратно эффективному количеству витков, хотя реально — это просто взаимодействие витков в том же самом поле. Если бы катушка увеличивала магнитный поток своим потокосцеплением, то можно было бы создавать умножители магнитного поля на катушке даже без тока, ибо потокосцепление не подразумевает замкнутости цепи катушки, но лишь совместную геометрию близости витков.
Часто реальное распределение потокосцепления по виткам катушки неизвестно, но его можно принять равномерным и одинаковым для всех витков, если реальную катушку заменить эквивалентной с другим числом витков w э , сохраняя при этом величину потокосцепления Ψ = w э Ф m , где Ф m — поток, сцепляющийся с внутренними витками катушки, а w э — эквивалентное или эффективное число витков катушки. Для рассмотренного на рис. 4 случая w э = Ψ/Ф 4 =48/8=6.
Можно также произвести замену реальной катушки на эквивалентную с сохранением числа витков Ψ = w Ф n . Тогда для сохранения потокосцепления необходимо принять, что со всеми витками катушки сцепляется магнитный поток Ф n = Ψ/ w .
Первый вариант замены катушки эквивалентной сохраняет картину магнитного поля, изменяя параметры катушки, второй — сохраняет параметры катушки, изменяя картину магнитного поля.
ПОТОКОСЦЕПЛЕНИЕ И ИНДУКТИВНОСТЬ КАТУШКИ
Если через катушку проходит изменяющийся ток, то ее витки пересекаются переменным магнитным полем, вызываемым этим током, и на концах катушки возникает ЭДС индукции. Для количественной характеристики этого процесса вводятся понятия потокосцепления и индуктивности катушки. На рис .2.13 по-казана катушка с током, витки которой пронизывают различное число силовых линий, следовательно, магнитные потоки различных витков различны. Эти магнитные потоки называют потоками самоиндукции, а их сумму для всех витков катушки называют потокосцеплением самоиндукции (ψ).




Рис. 2.13 Рис. 2.14 Рис. 2.15.
В том случае, когда магнитная проницаемость среды постоянна, между потокосцеплением и создающим его током существует линейная зависимость
где L – коэффициент пропорциональности называемый индуктивность ка- тушки. Единицей индуктивности является генри (Гн): На практике, как пра- вило, пользуются более мелкими единицами: миллигенри (1 мГн=10 -3 Гн) и
микрогенри (1 мГн=10 -6 Гн).
Индуктивность цилиндрической катушки, у которой длина достаточно велика
по сравнению с диаметром также может быть определена по формуле:
L = μ0 S w 2 / l (2.16)
Так как eL = – dΨL /dt и ΨL = Li для катушки без ферромагнитного сердечника ( L=const) окончательно получим:
eL = -L di /dt (2.17)
ЭДС eL называют ЭДС самоиндукции, а рассмотренное явление возникно-вения ЭДС в катушке вследствие изменения тока в этой катушке – само индукцией. ЭДС самоиндукции, согласно принципу Ленца, препятствует изменению тока в катушке, поэтому ток достигает установившегося значе- ния постепенно. Для нахождения всей энергии, которая накопится в магнитном поле катушки за время dt при изменении тока от 0 до I, проинтегрируем выражение L di/dt и получим:
WL = L I 2 / 2 (2.18)
В том случае, когда переменное магнитное поле созданное током одной катушки, пересекает витки, другой катушки (рис. 2.14), и наоборот, на зажимах последней катушки возникает ЭДС, которую называют ЭДС взаимоиндукции.
Магнитные потоки взаимоиндукции, пропорциональны токам, их созда- ющим, следовательно, и потокосцепление взаимоиндукции пропорциональны этим токам:
Ψ12 = M12 i1 , Ψ21 = M21 i2 (2.19)
Коэффициенты пропорциональности М.ч и М2 называют взаимными индуктивностями. В том случае, когда катушки не содержат ферромаг-нитных сердечников, M12.= M21 i2 = M. Взаимная индуктивность M зависит от числа витков катушек, их размеров и взаимного расположения, а также
от магнитных свойств среды. Единица взаимной индуктивности M генри (Гн) При изменении потокосцепления взаимоиндукции первой катушки во второй катушке наводится ЭДС взаимоиндукции:
e12 = – dΨ12 /dt = -M di1 /dt (2.20)
Соответственно изменение потокосцепления взаимоиндукции второй катушки вызывает ЭДС взаимоиндукции в первой катушке
e2 1 = – dΨ2 1 /dt = -M di2 /dt (2.21)








Явление взаимоиндукции находит широкое применение в различных электро и радиотехнических устройствах. В частности, оно используется для транс- формации электроэнергии в целях переменного тока. Однако это явление может проявлять себя и как вредное. Например, в сердечнике катушки или трансформатора (рис.2.15) за счет явления взаимоиндукции возникает кольцевой ток, который называют вихревым. Протекание вихревых токов в сердечнике вызывает большие тепловые потери. Для уменьшения этих потерь ферромагнитные сердечники набирают из тонких изолированных друг от друга листов электротехнической стали с повышенным удельным электричес -ким сопротивлением.
Ток или поток? Магнитные цепи и их основные характеристики
Привет, Хабр! С недавнего времени я стал задумываться об актуальности статей и заметил, что на Хабре нет ни одной обзорной статьи про магнитные цепи. Как так!? Ведь это. а что это такое?
Действительно, наверняка даже самые отстраненные от инженерного дела люди имеют представление о том, что такое электрические цепи, но возможно, что про магнитные цепи не слышали вовсе. Каждый школьник когда-то в учебнике физики наблюдал разные схемы и формулы, описывающие законы Ома. Но магнитные цепи в рамки школьного курса не входят.
Я решил написать данную статью, чтобы показать, насколько удивителен мир физики и заинтересовать школьников в её изучении. В данной статье, однозначно, для полноты вещей будут и выводы формул и использование некоторых математических операций, которые могут быть известны не всем, но такие моменты я постараюсь сгладить. Приступим!
Что нужно вспомнить?
Для более четкого представления сей статьи, неплохо бы вспомнить основные характеристики самого магнитного поля: вектор магнитной индукции, вектор напряженности, поток вектора магнитной индукции — а также нужно вспомнить немного про магнитные вещества, а именно про ферромагнетики.

Полагается, что вам известен обобщенный закон Ома и помнится, что такое ток, напряжение и сопротивление. Если нет, то крайне советую обратиться к сторонним ресурсам, чтобы иметь хотя бы общее представление о том, что последует далее. Крайне советую учебник И.Е. Иродова «Электромагнетизм» .
Применение магнитных цепей
Магнитные цепи находят очень большое поле применения, а именно, они используются для надежного пропускания магнитного потока по специальному проводнику с минимальными или, в некоторых случаях, определенными потерями. В электротехнической промышленности широко используется взаимная зависимость магнитной и электрической энергий, переход из одного состояния в другое. На подобном принципе работают, например, трансформаторы, разные электродвигатели, генераторы и другие устройства.

Конечно, можно продолжительное время говорить об устройствах, разных типах магнитопроводов (про которые речь пойдет далее), но наша первичная цель — рассмотреть выводы основных характеристик магнитных цепей. Продолжаем!
Как устроены магнитные цепи?
Магнитную цепь, на самом деле, не так сложно представить, как может показаться человеку, который о них впервые слышит. Обычно магнитные цепи представляют из себя некоторые фигуры из ферромагнитного сердечника с источником или несколькими источниками ПОтока. Пожалуй, один из самых простых примеров с одним источником, который можно взять на вооружение, проиллюстрирован ниже:

Перед продолжением обусловимся, что среди электротехников сердечник называют магнитопроводом. Часть магнитопровода, на которой отсутствуют обмотки и которая служит для замыкания магнитной цепи, называется «ярмо».
Начнем с тороидального сердечника. Такой тороидальный сердечник может служить формой для катушки, как бы странно это не звучало. Но что за катушка? Ну, первое что приходит в голову — провод, образующий витки. Хорошо, но какого его предназначение? Вернемся к электрическим цепям и вспомним, что существуют источники тока / напряжения, так называемые активные элементы. Так вот, в магнитных цепях роль источника выполняют катушки с током, накрученные на основной элемент магнитной цепи — ферромагнитный магнитопровод.
Вспомним теперь про ферромагнитные материалы. Почему именно они? Дело в том, что благодаря высокому значению магнитной проницаемости, что сигнализирует о хорошей намагниченности ферромагнетика, силовые линии магнитного поля практически не выходят за пределы сердечника, либо не выходят вовсе. Однако это будет справедливо лишь тогда, когда наш сердечник замкнутый, либо имеет небольшие зазоры. То есть, ферромагнетики обладают сильно выраженными магнитными свойствами, когда как у парамагнетиков и диамагнетиков они значительно слабее, что можно наблюдать на следующем графике зависимости намагниченности от напряженности магнитного поля:

Вещества, которые входят в конструкцию магнитопровода, могут обладать не только сильномагнитными свойствами, но также и слабомагнитными. Однако мы рассматриваем сердечник из ферромагнитного материала.
Ещё из школьного курса мы представляем себе картину с линиями магнитной индукции соленоида, мы можем визуально представить его поле и понимаем, что концентрация силовых линий, их насыщенность, наибольшая в центре рассматриваемого соленоида. Тут очень важно вспомнить правило буравчика, чтобы правильно указать направление силовых линий.
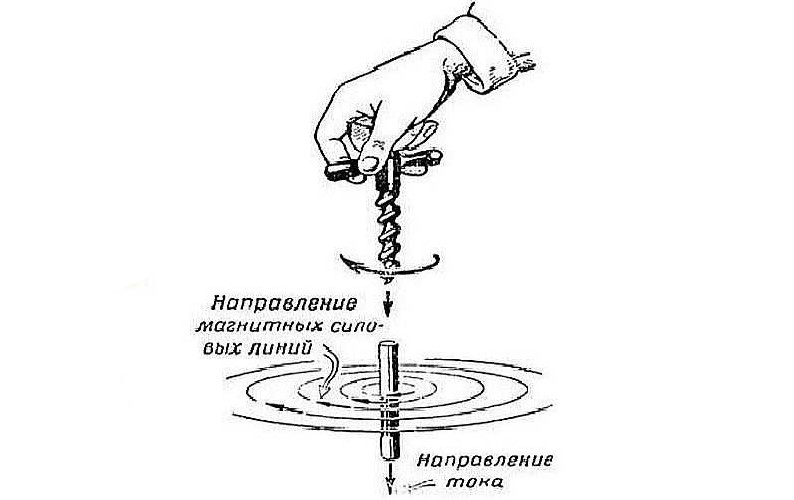
Отсюда становится ясно, что катушки-источники порождают магнитное поле, а следовательно и поток линий магнитной индукции. Такие линии будут циркулировать по нашему сердечнику, словно повторяя его форму. Именно поэтому нам важно условие замкнутости сердечника и материал, из которого он сделан. Положим, что наш воображаемый сердечник замкнут. Из этого следует, что и силовые линии замкнуты, а следовательно выполняется теорема Гаусса для магнитного поля, которая гласит: поток линий магнитной индукции через замкнутую поверхность равен нулю. Стоит учесть, что поток адаптируется под площадь сечения.*

Ну и в конечном счете ферромагнитный сердечник поток куда-то передает! Аналогичным образом замкнутый проводник позволяет передать электрический ток.
Отлично! Мы разобрались с тем, что такое магнитные цепи и даже вспомнили про теорему Гаусса и ферромагнетики. Теперь поговорим о том, какие следствия вытекают из теоремы Гаусса и возможности пренебрежения полем вне сердечника и в зазорах.
1] Магнитные потоки Ф1 и Ф2 через произвольные сечения будут равны между собой.
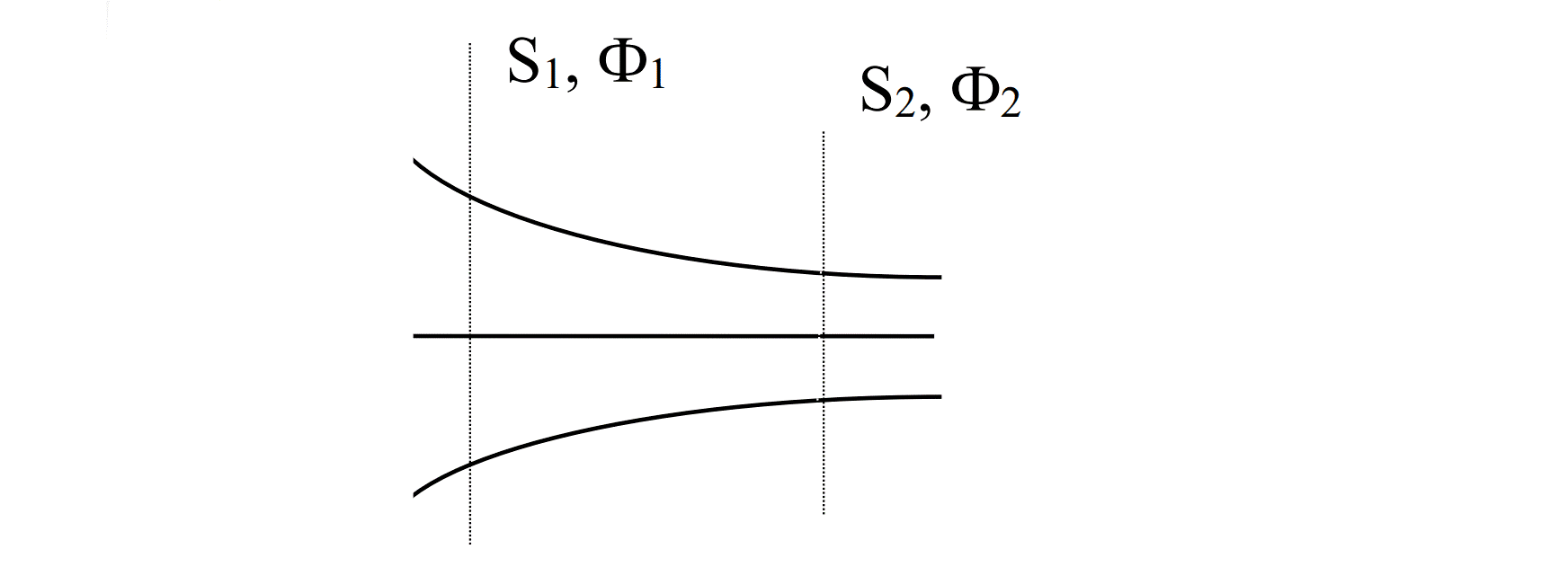
2] В узле (разветвлении) сердечника алгебраическая сумма потоков (с учетом их направлений) будет равна нулю. Мне одному это что-то напоминает?
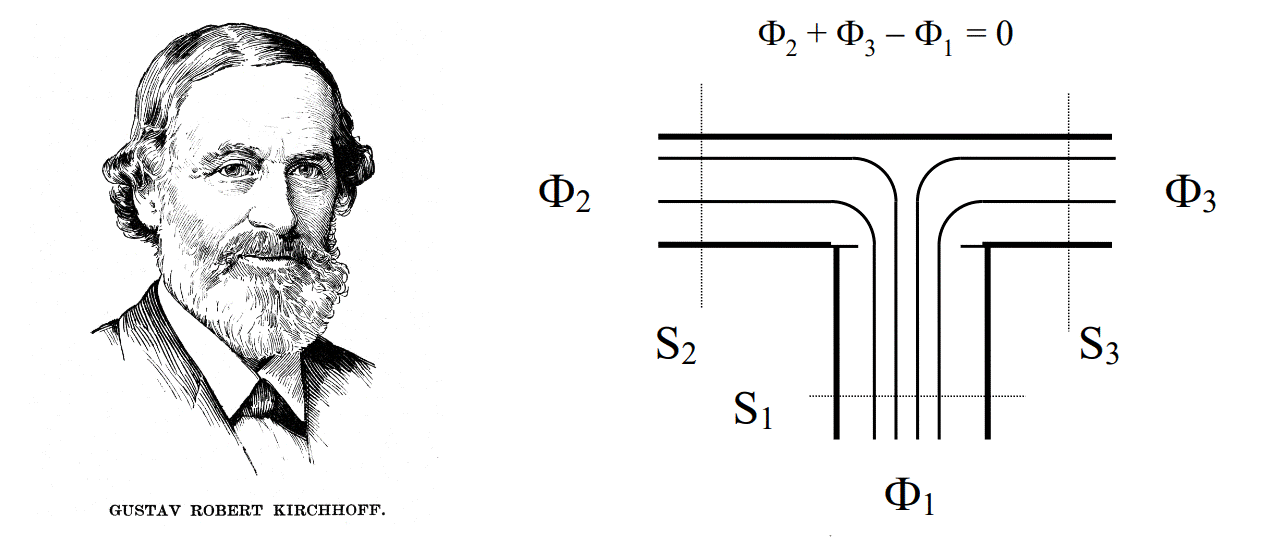
То есть мы окончательно сформулировали, что замкнутая (или почти замкнутая) система из ферромагнитных сердечников может рассматриваться как проводящая цепь. В нашем случае — магнитная.
Расчет магнитных цепей
Теперь внимание. Мы можем провести прямую аналогию и рассматривать магнитный поток в цепи, как характеристику электрической цепи — силу тока. Рассмотренное второе следствие означает, что для магнитной цепи, также как и для электрической, справедливо первое правило Кирхгофа. Отсюда можно лаконично перейти к закону полного тока, который в рамках классического магнетизма будет выглядеть следующим образом (приготовьтесь, немного математики):
Криволинейный интеграл по замкнутому контуру от напряженности магнитного поля будет равен алгебраической сумме токов, сцепленных (окруженных) данным контуром.

Также мы помним, что напряженность магнитного поля связана с магнитным потоком следующим образом:
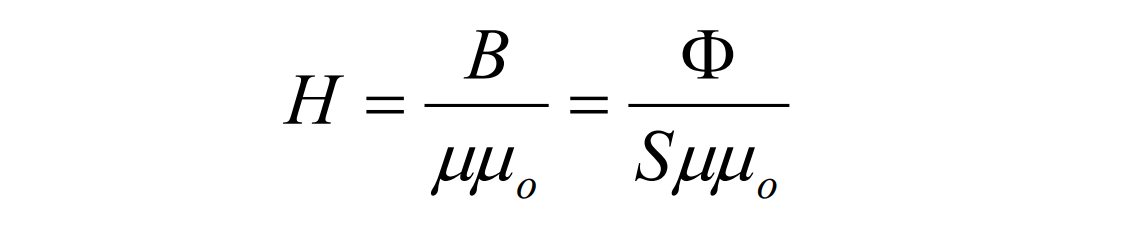
Руководствуясь приведенным законом полного тока и определением напряженности через магнитный поток, мы можем переписать закон полного тока относительно магнитного потока.

Откуда в уравнении появился и что символизирует аргумент l? Все просто. Так как мы рассматриваем контур L, то логично предположить, что на разных его участках наши показатели могут принимать разные значения: площадь сечения может изменяться, как и магнитная проницаемость или магнитный поток.
Полученное уравнение можно рассматривать как второй закон Кирхгофа, который, напомню, звучит следующим образом:
В любой момент времени алгебраическая сумма напряжений на ветвях контура равна нулю.
Для полной ясности, проведем аналогию между электрическими и магнитными цепями, а также их величинами.

Именно проведя аналогичное представление для электрической цепи, мы можем рассчитывать магнитные цепи. Для того, чтобы это сделать, следует:
Мысленно разбить сердечник на отдельные однородные участки (непрерывные, с постоянным сечением) без разветвлений и определить их магнитные сопротивления;
Построить эквивалентную электрическую цепь, последовательно заменяя участки магнитной цепи участками электрической с электрическими сопротивлениями, а также заменяя индуктивности (катушки) на источники ЭДС;
После обозначения заданных сопротивлений и ЭДС, можем вычислить в общем токи в элементах электрической цепи;
Произвести замену полученных величин согласно таблице (токи в потоки, ЭДС в МДС [Магнитодвижущую силу / Ампер-витки], а электрическое сопротивление в магнитное сопротивление).
Именно таким образом, мы можем рассчитать характеристики магнитной цепи. Полученные результаты позволяют, например, вычислить индуктивности.
А примеры расчетов будут?
Здесь — нет. А по ссылке — да! В данном документе Самарского государственного технического университета рассмотрены базовые примеры, которые позволят лучше разобраться в теме, если она вас заинтересовала. Помимо всего прочего, там же приведены теоретические справки. Советую прочитать в надежде, что вы сможете для себя что-то новое подчерпнуть.
Заключение
Во-первых, спасибо, что дочитали статью! Один из способов поддержать меня как автора — подписаться на мой паблик Вконтакте, где иногда выходят «локальные статьи».
Во-вторых, вернемся к началу статьи. Там я задался целью показать, почему физика удивительна. Не хочу быть многословным, поэтому просто попрошу вспомнить все то, что было описано выше. Мы оперировали моделями, которые относятся к разделу физики электричества и перенесли их на физику магнетизма. Наверняка, вы замечали, насколько часто встречаются элементы механики в иных разделах. Это по истине удивительно! Однако главное не поработиться иллюзией, что в мире все законы нам предельно известны.