Эквивалентный генератор эдс схема
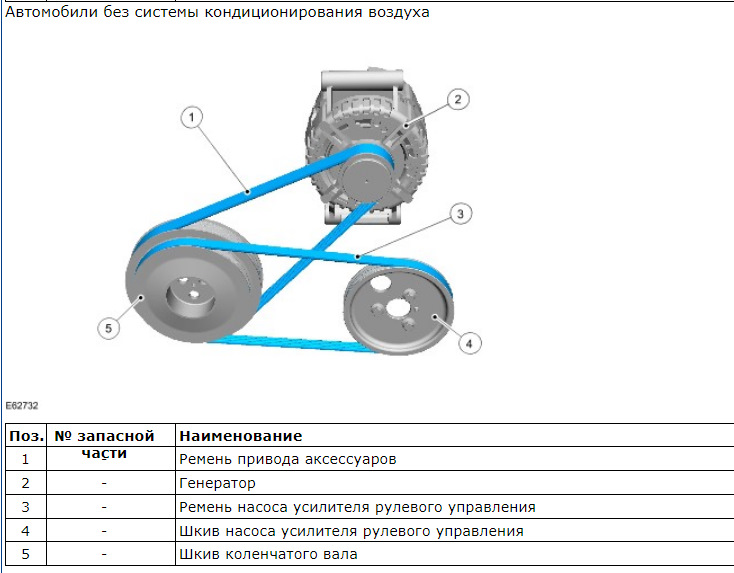
1.5 Метод эквивалентного генератора (метод эквивалентного источника ЭДС)
1.5 Метод эквивалентного генератора (метод эквивалентного источника ЭДС)
Метод эквивалентного генератора основан на теореме об эквивалентном источнике (теорема Тевенена) – активном двухполюснике.
Теорема Тевенена для линейных электрических цепей утверждает, что любая электрическая цепь, имеющая два вывода и состоящая из комбинации источников напряжения, источников тока и резисторов (сопротивлений), с электрической точки зрения эквивалентна цепи с одним источником напряжения E и одним резистором R, соединенными последовательно.
В методе эквивалентного генератора (метод эквивалентного источника ЭДС) сложную разветвленную схему рассматривают как активный двухполюсник по отношению к ветви R с искомым током I, который определяют по выражению
EЭГ = Uхх – ЭДС эквивалентного генератора равная напряжению холостого хода между зажимами подключенного пассивного элемента R в ветви с искомым током;
RЭГ = Rвх – сопротивление эквивалентного генератора равное входному сопротивлению пассивного двухполюсника относительно разомкнутых зажимов.
Алгоритм метода эквивалентного генератора (метод эквивалентного источника ЭДС)
1. Определяют напряжение холостого хода Uхх. Для этого ветвь с искомым током разрывают, удаляя сопротивление, и оставляют ЭДС в этой ветви, если она имеется.
2. Задаются направлением токов в ветвях оставшейся схемы после размыкания ветви. Записывают выражение для напряжения Uхх между разомкнутыми зажимами по второму закону Кирхгофа. В это уравнение войдет ЭДС разомкнутой ветви.
3. Рациональным методом рассчитываются токи в схеме, вошедшие в выражение напряжения Uхх.
4. Определяют входное сопротивление двухполюсника относительно разомкнутых зажимов.
5. В соответствии с методом эквивалентного генератора (метод эквивалентного источника ЭДС), определяют искомый ток ветви.
Решение задач методом эквивалентного генератора (методом эквивалентного источника ЭДС)
Задача 1.5.1 В схеме рис. 1.5.1 амперметр показывает 0,5 А. Определить его показания в схеме рис. 1.5.2.
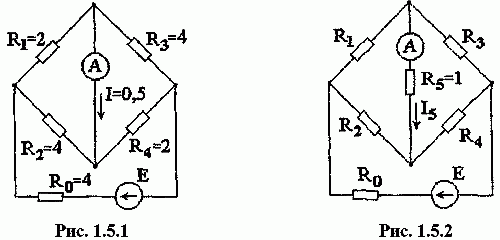
Решение. Можно считать, что в схеме рис. 1.5.2 резистор R5 подключен к зажимам эквивалентного генератора, который в схеме рис. 1.5.1 работает в режиме короткого замыкания.
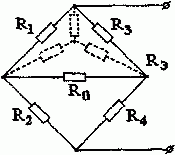
Определим внутреннее сопротивление эквивалентного генератора по схеме рис. 1.5.3, где заменим треугольник сопротивлений R1R3R0 эквивалентным соединением звездой
R 13 = R 1 ⋅ R 3 R 1 + R 3 + R 0 = 2 ⋅ 4 2 + 4 + 4 = 0,8 О м ; R 01 = R 1 ⋅ R 0 R 1 + R 3 + R 0 = 4 ⋅ 2 2 + 4 + 4 = 0,8 О м ; R 03 = R 0 ⋅ R 3 R 1 + R 3 + R 0 = 4 ⋅ 4 2 + 4 + 4 = 1,6 О м ; R Э = R 13 + ( R 01 + R 2 ) ⋅ ( R 03 + R 4 ) ( R 01 + R 2 ) + ( R 03 + R 4 ) = = 0,8 + ( 0,8 + 4 ) ⋅ ( 1,6 + 2 ) ( 0,8 + 4 ) + ( 1,6 + 2 ) = 2,86 О м .
ЭДС эквивалентного генератора определим из формулы I = EЭГ/ (RЭГ + R) метода эквивалентного генератора. При коротком замыкании I = EЭГ/RЭГ. Откуда ЭДС эквивалентного генератора
E Э = I ⋅ R Э = 0,5 ⋅ 2,86 = 1,43 В .
Ток I5 в схеме рис. 1.5.2 по методу эквивалентного генератора (методу эквивалентного источника ЭДС)
I 5 = E Э R Э + R 5 = 1,43 2,86 + 1 = 0,371 А .
Метод эквивалентного источника напряжения, метод эквивалентного источника тока, метод активного двухполюсника в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи
 метод эквивалентного генератора, метод эквивалентного источника ЭДС, теорема об эквивалентном источнике, теорема Тевенена
метод эквивалентного генератора, метод эквивалентного источника ЭДС, теорема об эквивалентном источнике, теорема Тевенена
Применение метода эквивалентного генератора для цепей переменного тока
Вы будете перенаправлены на Автор24
Алгоритм расчета цепи переменного тока методом эквивалентного генератора
Метод эквивалентного генератора – это метод преобразования электрической цепи, при использовании которого схемы из нескольких ветвей с источниками электродвижущей силы приводятся к одной ветви с эквивалентным значением.
Метод эквивалентного генератора позволяет вычислить ток только в одной ветви, поэтому расчет повторяется несколько раз (столько раз, сколько ветвей содержится в рассматриваемой цепи). По отношению к рассчитываемой ветви двухполюсник заменяется эквивалентным генератором, у которого электродвижущая сила равняется напряжению холостого хода, образующегося на зажимах данной ветви. При этом внутреннее сопротивление равно сопротивлению двухполюсника. Рассмотрим схему на рисунке ниже.
Рисунок 1. Схема. Автор24 — интернет-биржа студенческих работ
Если мы будем рассчитывать ветвь –Е1R1, то остальную часть схемы можно заключить в прямоугольник, которая и будет являться эквивалентным генератором. Тогда ток в рассматриваемой цепи можно рассчитать при помощи закона Ома:
$I = (Ег + –Е) / Rг + R$
Знак в выше представленном выражении зависит от направления электродвижущей силы в рассчитываемой ветви.
Электродвижущая сила – это способность источника тока создавать разность потенциалов.
Готовые работы на аналогичную тему
Алгоритм расчета выглядит следующим образом:
- Сначала из схемы удаляется цепь, которая была выбрана для расчета. Обозначаются узлы, к которым она присоединялась (обычно m и n). Остальная часть схемы цепи будет представлять собой эквивалентный генератор с эквивалентной электродвижущей силой и сопротивлением. Затем эти два параметра рассчитываются.
- Определяется эквивалентное сопротивление генератора. Чтобы это сделать, источник электродвижущей силы закорачивается (заменяется на отрезок провода), а ветви с источниками тока обрываются. После этого рассчитываются входные сопротивления оставшейся части схемы относительно зажимов m и n.
- Для расчета электродвижущей силы генератора выбирается путь от точки m до точки n, так, чтобы он не проходил через ветви с источниками тока, на всем пути отмечаются точки падения напряжения.
- После этого, зная сопротивление генератора и эквивалентную электродвижущую силу, рассчитывается искомый ток.
Применение метода эквивалентного генератора для цепей переменного тока
Рассмотрим схему на рисунке ниже.
Рисунок 2. Схема. Автор24 — интернет-биржа студенческих работ
Допустим, что необходимо определить ток I3, при условии, что нам известны значения сопротивлений и электродвижущих сил рассматриваемой цепи. Для расчета искомого тока обрываем цепь и обозначаем узлы m и n, как показано на рисунке ниже.
Рисунок 3. Схема. Автор24 — интернет-биржа студенческих работ
Оставшаяся часть рассматриваемой схемы является эквивалентным генератором с эквивалентной электродвижущей силой и сопротивлением. Рассчитываем эквивалентное сопротивление генератора. Для этого закорачиваются источники электродвижущей силы закручиваются, а ветви, в состав которых входят источники тока обрываются, как на рисунке ниже.
Рисунок 4. Схема. Автор24 — интернет-биржа студенческих работ
Входное сопротивление относительно зажимов можно рассчитать следующим образом:
$Rг = ((R2 • R3) / (R2 + R3)) + R4+R6$
Для расчета эквивалентной электродвижущей силы генератора, выбирается путь от точки m до точки n, таким образом, чтобы он не проходил ветви, в которых есть источники тока, как показано на рисунке ниже.
Рисунок 5. Схема. Автор24 — интернет-биржа студенческих работ
$Ег = Umn = U2 + U4 + U6 — E2$
Необходимо рассчитать данные напряжения. Так как рассматриваемая схема состоит из двух независимых контуров, то их можно рассчитать по отдельности. Составляются уравнения для второго контура согласно второму закону Кирхгофа:
Из второго контура, где протекает ток источника J определяются следующие напряжения:
Минусы в формулах означают, что направления рассчитываемых напряжений выбраны таким образом, что они противоположны направлениям протекающих токов. Так как нам теперь известны эквивалентная электродвижущая сила и сопротивление генератора, то искомый ток может быть рассчитан по следующей формуле:
Теперь определим ток I4 в этой же схеме. Обрываем цепь и обозначаем напряжение между точками m и n b и получаем:
Рисунок 6. Схема. Автор24 — интернет-биржа студенческих работ
Для определения сопротивления получившегося генератора, обрывается ветвь с источником тока и закорачиваются источники электродвижущей силы, как на рисунке ниже.
Рисунок 7. Схема. Автор24 — интернет-биржа студенческих работ
$Rг = ((R / R3) / (R2 + R3)) + R1$
Выбираем направление пути от точки m к n, аналогичным образом, как для расчета I3 (в обход ветвей с источниками тока). Выбранный путь изображен на рисунке ниже
Рисунок 8. Схема. Автор24 — интернет-биржа студенческих работ
Получается, что эквивалентная электродвижущая сила генератора может быть рассчитана следующим образом:
$Ег = Umn = U1 + U2$
Напряжение U1 равно:
Напряжение U2 можно рассчитать только при условии, что ветвь с источником Е1 подключена параллельно:
Рисунок 9. Схема. Автор24 — интернет-биржа студенческих работ
Получившаяся схема на рисунке ниже позволяет рассчитать напряжение U2
Рисунок 10. Схема. Автор24 — интернет-биржа студенческих работ
$U2 = ((E1 + Eэ) / (R + R3)) • R2$
Получив значение Eг, можно рассчитать искомый ток:
$I4 = (Eг + E2) / (R4 + R6 + Rг)$
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи
![]()
Эксперт по предмету «Электроника, электротехника, радиотехника» , преподавательский стаж — 5 лет
Эквивалентный генератор






Эквивалентный генератор
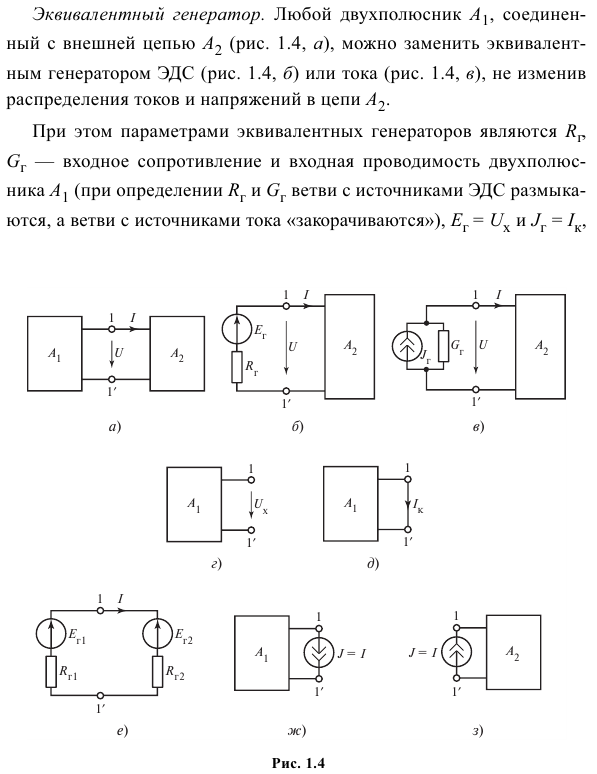
Эквивалентный генератор. Двухполюсник А1, подключенный к внешней цепи А2 (рис. 1.4, а), может быть заменен эквивалентным ЭДС-генератором (рис. 1.4, б) или током (рис. 1.4, в). Схема А2.
В этом случае параметрами эквивалентного генератора являются Rg, Gg — входное сопротивление и входная проводимость диполя А1 (ветвь, где источник ЭДС открыт, а источник тока «закорочен» при определении Rg и Gg).
Напряжение разомкнутой цепи (рисунок 1.4, d) и ток короткого замыкания клеммы A1 Ik-2 (рисунок 1.4, e).
Замена двухполюсника А1 (рис. 1.4, а) эквивалентным ЭДС-генератором (рис. 1.4, б) или током (рис. 1.4, в) упрощает начальную цепь (см. Рис. 1.4, а).
Метод расчета схемы, основанный на аналогичном упрощении схемы, называется методом эквивалентного генератора.
При решении задач электротехники часто необходимо знать режим работы одной конкретной ветви, а не всей цепи.
Существует эквивалентный генераторный метод для определения параметров такой ветви.
Суть метода эквивалентного генератора заключается в том, чтобы найти ток в одной выбранной ветви.
- С другой стороны, остальная часть сложной электрической цепи заменяется эквивалентной ЭДС Eeq с reeq внутреннего сопротивления.
В этом случае часть схемы, которая содержит источник ЭДС, называется эквивалентным генератором или активной двухполюсной сетью, поэтому это имя метода.
- Решение задач по электротехнике тоэ
| Фундаментальная система уравнений электрической цепи | Диакоптика расчет по частям электрических цепей |
| Узловые и контурные уравнения | Принцип наложения суперпозиции |






















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Суть метода эквивалентного генератора
Метод эквивалентного генератора (МЭГ) применяется, когда есть некая нагрузка, подключённая к сложной активной цепи. При этом активная цепь сама по себе интереса не представляет, но необходимо учесть её влияние на нагрузку, на которую направлен фокус. С помощью данного метода активная цепь преобразуется в очень простой вид – в одну ветвь с эквивалентной ЭДС Eэкв и с эквивалентным сопротивлением Zэкв.
Воспользуйтесь программой онлайн-расчёта электрических цепей. Программа позволяет рассчитывать электрические цепи по закону Ома, по законам Кирхгофа, по методам контурных токов, узловых потенциалов и эквивалентного генератора, а также рассчитывать эквивалентное сопротивление цепи относительно источника питания.
Суть метода эквивалентного генератора [1]
Пример того, как это делается, приведён на рис. 1. Самое важное здесь то, что ток в нагрузке что в исходной цепи, что в преобразованной, одинаковый. Именно в этом смысле эквивалентный генератор и эквивалентен исходной активной цепи.
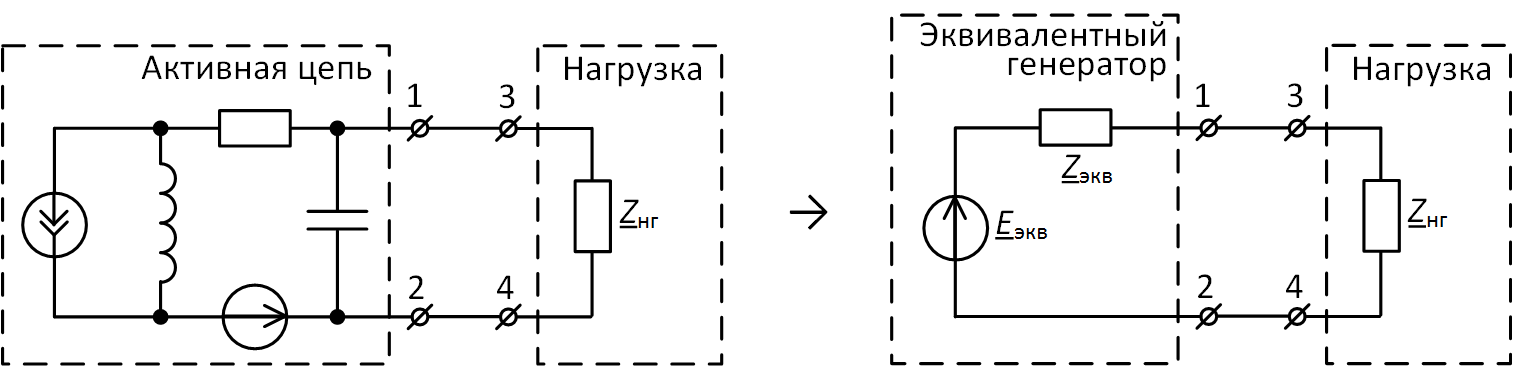
Рис. 1. Преобразование активной цепи в эквивалентный генератор
МЭГ применяется для решения самых разнообразных задач. Например, он используется в электроэнергетике, когда нужно рассчитать различные режимы сети. Конкретно используется для того, чтобы эквивалентировать всю внешнюю сеть по отношению к рассчитываемой, и тем самым упростить расчёт. Также часто бывает, что о внешней сети вообще мало что известно, и в этих условиях расчётчики просто вынуждены довольствоваться одним только эквивалентным генератором.
Эквивалентная ЭДС Eэкв и с эквивалентное сопротивление Zэкв в зависимости от решаемой задачи могут быть определены двумя способами:
- расчётом активной цепи с отключённой от неё нагрузкой;
- опытным путём, с помощью опытов холостого хода (когда Zнг = ∞) и короткого замыкания (когда Zнг = 0).
Первым способом можно воспользоваться только тогда, когда вся активная цепь перед глазами и известны все её параметры. А когда эквивалентируемая цепь – это «чёрный ящик», на котором можно проводить опыты, работает второй способ. В чём заключаются оба эти способа – очень важная информация для усвоения каждого изучающего ТОЭ, но намного важней знания о том, почему они работают. Поэтому далее подробно рассмотрим из чего именно вытекает МЭГ.
Возьмём пример по рис. 1 и для начала изолируем эквивалентируемую активную цепь от нагрузки (рис. 2). Это будет режим холостого хода, когда тока в нагрузке нет. В этом режиме нас интересует напряжение Uхх между выводами 1 и 2. Такое же напряжение будет между выводами 1 и 3, если соединить между собой выводы 2 и 4 (см. рис. 3), поскольку ток в нагрузке при этом останется равным нулю и падение напряжения между выводами 3 и 4 также будет нулевым.
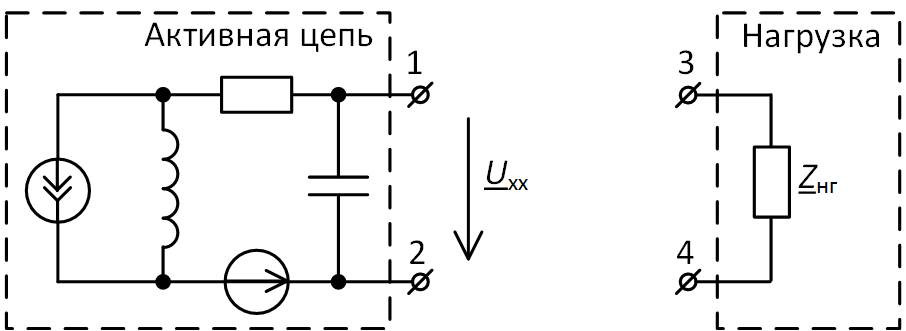
Рис. 2. Холостой ход эквивалентируемой цепи
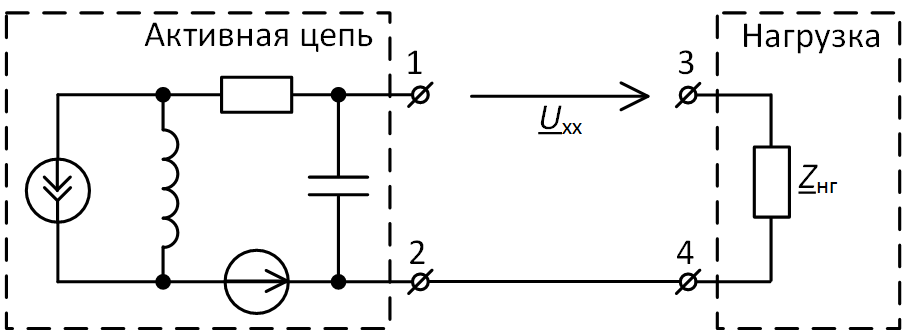
Рис. 3. Соединение выводов 2 и 4
Теперь очень важная мысль: если между выводами 1 и 3 включить ЭДС, равную Uхх, как это показано на рис. 4, то в результате ничего не изменится. Это очевидно, ведь такая ЭДС пытается поддержать между выводами 1 и 3 напряжение Uхх, а это было так и до её включения.
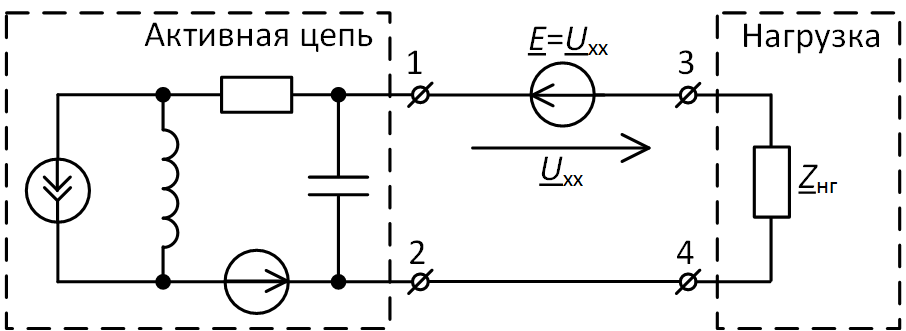
Рис. 4. Включение между выводами 1 и 3 ЭДС, равной Uхх
Далее, если рядом включить ещё такую же ЭДС, но с противоположным направлением, то в итоге получится исходная активная цепь с подключённой к ней нагрузке, как на рис. 1. Всё это проиллюстрировано на рис. 5.

Рис. 5. Включение между выводами 1 и 3 ещё одной такой же ЭДС с противоположным направлением
Применим принцип наложения и разложим получившуюся цепь с двумя ЭДС между выводами 1 и 3 на две части. Распределим между этими двумя частями все имеющиеся источники тока и ЭДС так, как это показано на рис. 6 (вспомним, что по принципу наложения исключаемые из одной из частей источники тока должны разрываться, а источники ЭДС – закорачиваться).
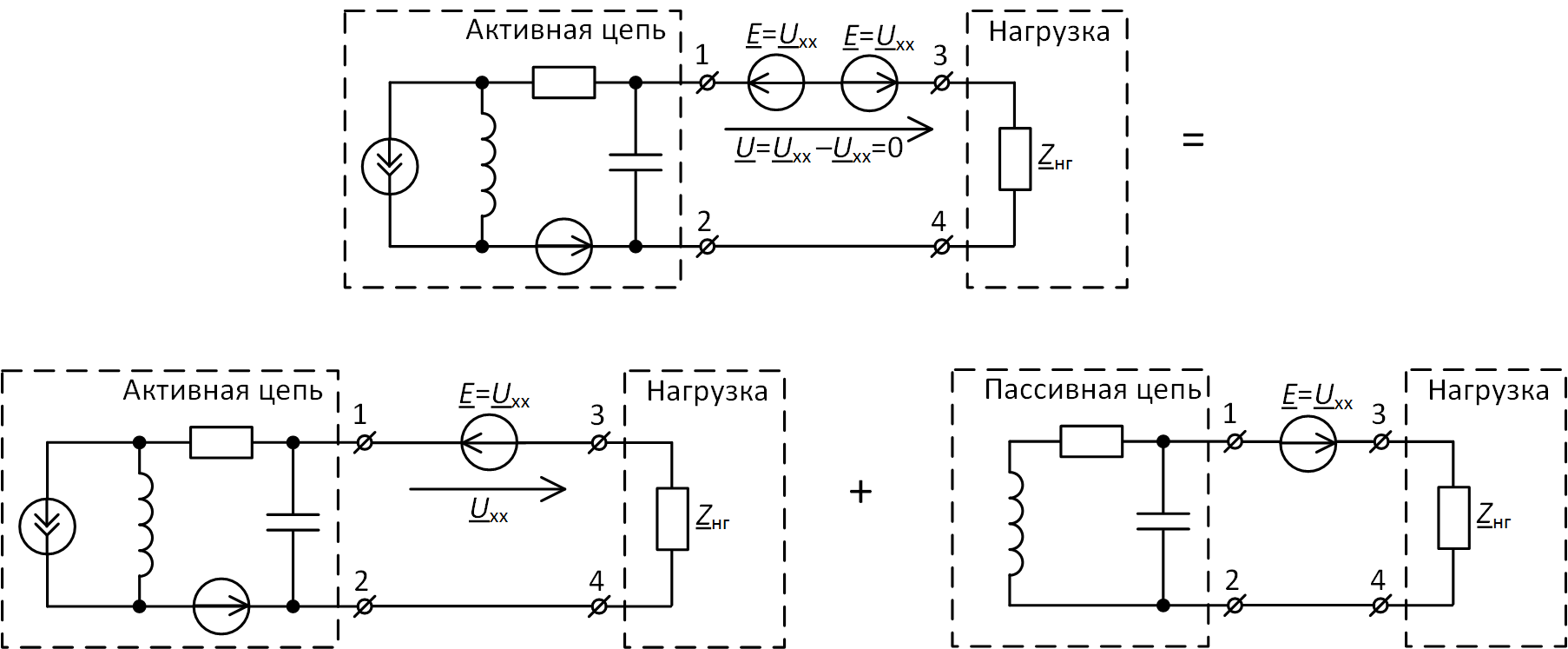
Рис. 6. Разделение активной цепи с нагрузкой на две части
Что имеем в итоге? Одну из частей мы уже видели на рис. 4, с точки зрения нагрузки это то же самое, что и на рис. 2, т.е. холостой ход. Для этой части ток в нагрузке получается нулевым, поэтому далее её можно исключить из рассмотрения. И выходит, что весь ток в нагрузке создаётся второй частью разделившейся цепи, она оказывается ей эквивалентной.
Далее дело техники преобразовать получившуюся пассивную цепь в эквивалентное сопротивление, затем объединить её с единственной в этой цепи ЭДС и получить таким образом то, что называется эквивалентным генератором (рис. 7).
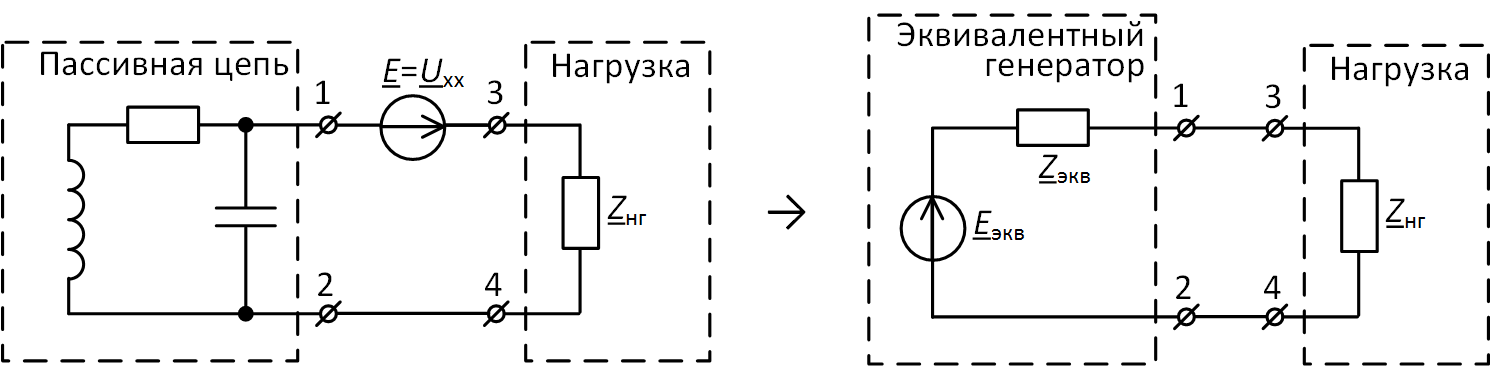
Рис. 7. Готовый эквивалентный генератор
Особенности метода эквивалентного генератора
- Т.к. МЭГ основан на принципе наложения, его можно применять только для линейных электрических цепей, для которых данный принцип работает. Для нелинейных цепей МЭГ применён быть не может.
- МЭГ работает на комплексных схемах замещения, т.е. только для какой-то одной частоты. Часто это бывают схемы для частоты сети (50 или 60 Гц) или это цепи постоянного тока (0 Гц).
- Из предыдущего замечания вытекает, что эквивалентные генераторы некорректно использовать в схемах расчёта переходных процессов в мгновенной форме.
- В качестве нагрузки эквивалентного генератора может выступать активная цепь. В этом случае нужно быть очень аккуратным при определении эквивалентной ЭДС.
Список использованной литературы
- Зевеке Г.В., Ионкин П.А., Нетушил А.В., Страхов С.В. Основы теории цепей. Учебник для вузов. Изд. 4-е, переработанное. М., «Энергия», 1975.
Рекомендуемые записи
Физически симметричные составляющие в электрических цепях не существуют. Симметричные составляющие введены для существенного упрощения расчёта…
Симметричные составляющие – очень важные параметры, используемые в релейной защите для реализации защит различного оборудования.…
При расчёте электрических цепей, в том числе для целей моделирования, широко применяются законы Кирхгофа, позволяющие…
Метод эквивалентного генератора
Этот метод основан на сформулированной выше теореме (см. подраздел 1.4) и применяется в тех случаях, когда требуется рассчитать ток в какой-либо одной ветви при нескольких значениях ее параметров (сопротивления и ЭДС) и неизменных параметрах всей остальной цепи.
Сущность метода заключается в следующем. Вся цепь относительно зажимов интересующей нас ветви представляется как активный двухполюсник, который заменяется эквивалентным генератором, к зажимам которого подключается интересующая нас ветвь. В итоге получается простая неразветвленная цепь, ток в которой определяется по закону Ома.
ЭДС ЕЭ эквивалентного генератора и его внутреннее сопротивление RЭ находятся из режимов холостого хода и короткого замыкания двухполюсника.
Порядок решения задачи этим методом рассмотрим на конкретном числовом примере.
Пример 1.5. В цепи, показанной на рис. 1.20, а, требуется рассчитать ток I3 при шести различных значениях сопротивления R3 и по результатам расчета построить график зависимости I3(R3).
Числовые значения параметров цепи: Е1 = 225 В; Е3 = 30 В; R1 = 3 Ом; R2 = 6 Ом.
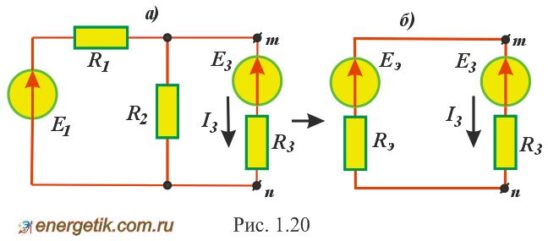
Р е ш е н и е. а) Расчет режима холостого хода.
Убираем третью ветвь, оставляя зажимы m и n разомкнутыми (рис. 1.21, а). Напряжение между ними, равное UX, находится как падение напряжения на сопротивлении R2:
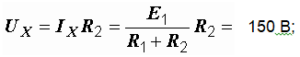
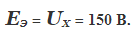
б) Расчет режима короткого замыкания. Замыкаем накоротко зажимы m и n (рис. 1.21, б). Ток короткого замыкания 75 А.
Внутреннее сопротивление эквивалентного генератора:
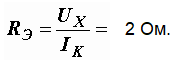
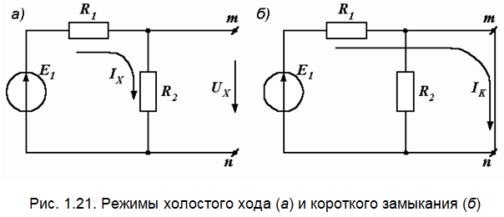
Величину RЭ можно найти и другим способом. Оно равно входному сопротивлению двухполюсника при равенстве нулю всех его ЭДС. Если на рис. 1.21, а мысленно закоротить зажимы ЭДС Е1, то сопротивления R1 и R2 окажутся соединенными параллельно, и входное сопротивление цепи относительно зажимов m и n будет равно: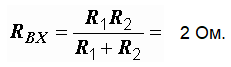
Ток в полученной неразветвленной цепи (рис. 1.20, б) определяется по закону Ома:
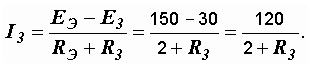
Подставляя в последнюю формулу требуемые значения сопротивления R3, вычисляем ток и строим график (рис. 1.22).
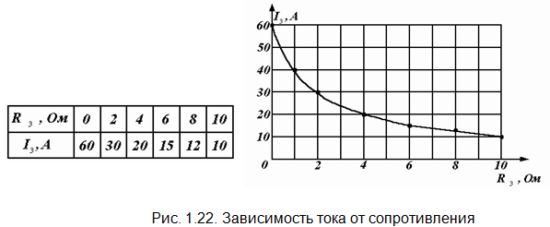
Данную задачу целесообразно решать именно методом эквивалентного генератора. Применение другого метода, например метода контурных токов, потребует решать систему уравнений столько раз, сколько значений тока необходимо найти. Здесь же всю цепь мы рассчитываем только два раза, определяя ЕЭ и RЭ, а многократно используем лишь одну простую формулу (1.13).
Лабораторная работа № 3 Метод эквивалентного генератора. Линейные соотношения между токами и напряжениями

Национальный исследовательский университет «МЭИ»


Кафедра Теоретических Основ Электротехники
Лабораторная работа № 3
Метод эквивалентного генератора.
Линейные соотношения между токами и напряжениями.
Л а б о р а т о р н а я р а б о т а № 3
МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА. ЛИНЕЙНЫЕ СООТНОШЕНИЯ МЕЖДУ ТОКАМИ И НАПРЯЖЕНИЯМИ
Краткое содержание работы
В работе теоретически и экспериментально находятся параметры эквивалентного генератора. Исследуются зависимости тока, напряжения и мощности приемника при изменении его сопротивления, а также линейные соотношения между токами ветвей в разветвленной электрической цепи.
Ключевые слова: линейная электрическая цепь; активный двухполюсник; схемы замещения двухполюсников; метод эквивалентного генератора; параметры эквивалентного генератора; формула (схема) Тевенена; формула (схема) Нортона; активная мощность двухполюсника
1. Теоретическая справка
При анализе сложных электрических цепей часто требуется определить ток и напряжение только в одной ветви. В этом случае используют метод эквивалентного генератора. Выделяют исследуемую ветвь (активную или пассивную), присоединенную к сложной цепи. Остальная часть цепи с двумя выделенными узлами представляет собой активный двухполюсник. По отношению к выделенной ветви активный двухполюсник можно преобразовать в эквивалентный генератор.
Теорема Тевенена – Гельмгольца: если активный двухполюсник, к которому присоединена выделенная ветвь, заменить источником ЭДС, равной напряжению на зажимах разомкнутой ветви и сопротивлением, равным входному сопротивлению, то ток в этой ветви не изменится.
Математическая формулировка теоремы для нахождения тока пассивной ветви ab выражается формулой Тевенена:
 .
.
Этому равенству соответствует расчетная схема (последовательная схема замещения активного двухполюсника), представленная на рис. 1:

Если выделенная ветвь содержит источник ЭДС, тогда расчетная схема будет иметь вид, представленной на рис. 2:

Применение теоремы об эквивалентном генераторе позволяет свести расчет сложной цепи к расчету одноконтурной и использовать для определения тока формулу Тевенена:  .
.
Алгоритм расчета по методу эквивалентного генератора:
1. Находят напряжение холостого хода  на зажимах разомкнутой ветви ab.
на зажимах разомкнутой ветви ab.
2. Определяют входное сопротивление двухполюсника, преобразуя его в пассивный (все внутренние источники ЭДС и тока принимают равными нулю).

3. Определяют искомый ток по формуле Тевенена.
Можно использовать формулу Нортона, соответствующую параллельной схеме замещения активного двухполюсника (рис 3):

 .
.
В данной работе сопротивление выделенной ветви может изменяться и определяется как нагрузка (Rн) по отношению к активному двухполюснику (эквивалентному генератору). При экспериментальном определении параметров эквивалентного генератора в данной работе используется режим холостого хода, в котором практически идеальным вольтметром ( ) измеряется напряжение холостого хода
) измеряется напряжение холостого хода  . Далее осуществляется режим короткого замыкания, в котором измеряется ток . По результатам измерения строят нагрузочную характеристику активного двухполюсника (эквивалентного генератора). Входное сопротивление может быть найдено из соотношения
. Далее осуществляется режим короткого замыкания, в котором измеряется ток . По результатам измерения строят нагрузочную характеристику активного двухполюсника (эквивалентного генератора). Входное сопротивление может быть найдено из соотношения  . По результатам измерений проводится проверка выполнения теоремы Тевенена.
. По результатам измерений проводится проверка выполнения теоремы Тевенена.
Передача энергии от активного двухполюсника к пассивному.
Определим условия, при которых мощность пассивного двухполюсника (приемника) максимальна. По теореме об эквивалентном генераторе ток и напряжение в приемнике R можно определить по расчетной схеме эквивалентного генератора (рис.1).
Напряжение  , мощность приемника
, мощность приемника  или
или  , мощность эквивалентного генератора
, мощность эквивалентного генератора  .
.
Если мощность приемника максимальна, то  , следовательно, ток приемника должен быть
, следовательно, ток приемника должен быть  . По формуле Тевенена
. По формуле Тевенена  , максимальная мощность выделяется в приемнике при
, максимальная мощность выделяется в приемнике при  . Максимальная мощность равна
. Максимальная мощность равна  .
.
Отношение мощности Pн к мощности Pг называется к. п.д. эквивалентного активного двухполюсника:
При  к. п.д.
к. п.д.  .
.
Графики зависимости Pн(Iн), Pг(Iн), Uн(Iн), η(Iн) представлены на рис. 4.

Согласно принципу линейности при изменении сопротивления резистивного элемента в одной из ветвей линейной электрической цепи все токи и напряжения связаны линейными соотношениями. При изменении сопротивления Rн токи i-ой и k-ой ветвей связаны линейным соотношением:
 .
.
Коэффициенты линейности a и b определяются из двух любых режимов при разных значениях сопротивления резистора и неизменности остальных параметров цепи.
2. Подготовка к работе
1. Рассчитать любым методом токи в цепи, схема которой представлена на рис. 5, при E1= 9 В и J2= 50 мА. Значения сопротивлений резисторов  и
и  даны в таблице 1,
даны в таблице 1,  Ом, Rн=R1. Определить напряжение Uн, мощность Pн.
Ом, Rн=R1. Определить напряжение Uн, мощность Pн.
2. Рассматривая цепь относительно резистора Rн как активный двухполюсник (эквивалентный генератор), рассчитать его параметры Uхх, Rвх, Iкз. Нарисовать последовательную и параллельную схемы замещения активного двухполюсника. Вычислить значение тока Iн при Rн=R1 по двум схемам замещения. Построить вольт-амперную характеристику активного двухполюсника Uн(Iн). Графически определить значение тока Iн и напряжения Uн при Rн=R1 и Rн=Rвх.

3. Определить величину сопротивления Rн, при котором в нем потребляется максимальная мощность. Вычислить Pmax. Построить график зависимости Pн(Iн).
4. Записать линейное соотношение I1(Iн)=aIн+b. Определить коэффициенты  и
и  по двум известным значениям токов (Rн
по двум известным значениям токов (Rн  и Rн=R1).
и Rн=R1).

-%D0%BD%D0%B0-%D1%84%D0%BE%D1%80%D0%B4-%D1%84%D1%8C%D1%8E%D0%B6%D0%BD,-%D1%84%D0%B8%D0%B5%D1%81%D1%82%D0%B0-%D0%BF%D1%80%D0%B8%D0%BD%D1%86%D0%B8%D0%BF%D1%8B-%D1%80%D0%B0%D0%B1%D0%BE%D1%82%D1%8B,-%D0%BE%D1%81%D0%BD%D0%BE%D0%B2%D0%BD%D1%8B%D0%B5-%D0%BD%D0%B5%D0%B8%D1%81%D0%BF%D1%80%D0%B0%D0%B2%D0%BD%D0%BE%D1%81%D1%82%D0%B8/assets/img/content/Fusion/durashift-esm.jpg)