Что можно сделать с генератором случайных чисел

Подробно о генераторах случайных и псевдослучайных чисел

Введение

Генераторы случайных чисел — ключевая часть веб-безопасности. Небольшой список применений:

• Генераторы сессий (PHPSESSID)
• Генерация текста для капчи
• Шифрование
• Генерация соли для хранения паролей в необратимом виде
• Генератор паролей
• Порядок раздачи карт в интернет казино

Как отличить случайную последовательность чисел от неслучайной?

Пусть есть последовательность чисел: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Является ли она случайной? Есть строгое определение для случайной величины. Случайная величина — это величина, которая принимает в результате опыта одно из множества значений, причём появление того или иного значения этой величины до её измерения нельзя точно предсказать. Но оно не помогает ответить на наш вопрос, так как нам не хватает информации для ответа. Теперь скажем, что данные числа получились набором одной из верхних строк клавиатуры. «Конечно не случайная» — воскликните Вы и тут же назовете следующие число и будете абсолютно правы. Последовательность будет случайной только если между символами, нету зависимости. Например, если бы данные символы появились в результате вытягивания бочонков в лото, то последовательность была бы случайной.

Чуть более сложный пример или число Пи

Последовательность цифры в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с какой-то неизвестной точки. Такой генератор, возможно и пройдет «тест на следующий бит», так как ПИ, видимо, является случайной последовательностью. Однако этот подход не является критографически надежным — если криптоаналитик определит, какой бит числа Пи используется в данный момент, он сможет вычислить и все предшествующие и последующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не должен иметь возможности предсказать работу генератора случайных чисел.

Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)

Источники энтропии используются для накопления энтропии с последующим получением из неё начального значения (initial value, seed), необходимого генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ использует единственное начальное значение, откуда и следует его псевдослучайность, а ГСЧ всегда формирует случайное число, имея в начале высококачественную случайную величину, предоставленную различными источниками энтропии.
Энтропия – это мера беспорядка. Информационная энтропия — мера неопределённости или непредсказуемости информации.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.

Уязвимости ГПСЧ

• Предсказуемая зависимость между числами.
• Предсказуемое начальное значение генератора.
• Малая длина периода генерируемой последовательности случайных чисел, после которой генератор зацикливается.

Линейный конгруэнтный ГПСЧ (LCPRNG)

Распространённый метод для генерации псевдослучайных чисел, не обладающий криптографической стойкостью. Линейный конгруэнтный метод заключается в вычислении членов линейной рекуррентной последовательности по модулю некоторого натурального числа m, задаваемой следующей формулой:

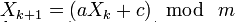
где a (multiplier), c (addend), m (mask) — некоторые целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при разных его значениях получаются различные последовательности случайных чисел.

Для выбора коэффициентов имеются свойства позволяющие максимизировать длину периода(максимальная длина равна m), то есть момент, с которого генератор зациклится [1].

Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Получается система уравнений

Решив эту систему, можно определить коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить самостоятельно или найти решение не получилось. Буду очень признателен за любую помощь в этом направлении.

Предсказание результатов линейно-конгруэнтного метода

Основным алгоритмом предсказания чисел для линейно-конгруэнтного метода является Plumstead’s — алгоритм, реализацию, которого можно найти здесь [4](есть онлайн запуск) и здесь [5]. Описание алгоритма можно найти в [9].
Простая реализация конгруэнтного метода на Java.

Отправив 20 чисел на сайт [4], можно с большой вероятностью получить следующие. Чем больше чисел, тем больше вероятность.

Взлом встроенного генератора случайных чисел в Java

Многие языки программирования, например C(rand), C++(rand) и Java используют LСPRNG. Рассмотрим, как можно провести взлом на примере java.utils.Random. Зайдя в исходный код (jdk1.7) данного класса можно увидеть используемые константы

Метод java.utils.Randon.nextInt() выглядит следующим образом (здесь bits == 32)

Результатом является nextseed сдвинутый вправо на 48-32=16 бит. Данный метод называется truncated-bits, особенно неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить методом грубой силы(brute-force).

Пусть мы знаем два подряд сгенерированных числа x1 и x2. Тогда необходимо перебрать 2^16 = 65536 вариантов oldseed и применять к x1 формулу:

до тех пор, пока она не станет равной x2. Код для brute-force может выглядеть так

Вывод данной программы будет примерно таким:

Несложно понять, что мы нашли не самый первый seed, а seed, используемый при генерации второго числа. Для нахождения первоначального seed необходимо провести несколько операций, которые Java использовала для преобразования seed, в обратном порядке.

И теперь в исходном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));

И всё, мы успешно взломали ГПСЧ в Java.

Взлом ГПСЧ Mersenne twister в PHP

Рассмотрим ещё один не криптостойкий алгоритм генерации псевдослучайных чисел Mersenne Twister. Основные преимущества алгоритма — это скорость генерации и огромный период 2^19937 − 1, На этот раз будем анализировать реализацию алгоритма mt_srand() и mt_rand() в исходном коде php версии 5.4.6.

Можно заметить, что php_mt_reload вызывается при инициализации и после вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Рассмотрим (s1 ^ (s1 >> 18)). В бинарном представление операция выглядит так:

10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что первые 18 бит (выделены жирным) остались без изменений.
Напишем две функции для инвертирования битового сдвига и xor

Тогда код для инвертирования последних строк функции php_mt_rand() будет выглядеть так

Если у нас есть 624 последовательных числа сгенерированных Mersenne Twister, то применив этот алгоритм для этих последовательных чисел, мы получим полное состояние Mersenne Twister, и сможем легко определить каждое последующее значение, запустив php_mt_reload для известного набора значений.

Область для взлома

Если вы думаете, что уже нечего ломать, то Вы глубоко заблуждаетесь. Одним из интересных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его особенностью является закрытость исходного кода и отсутствие задания seed’а. Основной интерес к нему, это использование во многих онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса доллара и заканчивая количеством времени проведенным в пробке каждый день. И найти закономерность в таких данных очень не простая задача.

Задание распределения для генератора псевдослучайных чисел

Для любой случайной величины можно задать распределение. Перенося на пример с картами, можно сделать так, чтобы тузы выпадали чаще, чем девятки. Далее представлены несколько примеров для треугольного распределения и экспоненциального распределения.

Треугольное распределение

Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.

В данном случае мы берем случайную величину rand() и задаем ей распределение, исходя из функции треугольного распределения. Для параметров a = -40, b = 100, c = 50 график 10000000 измерений будет выглядеть так

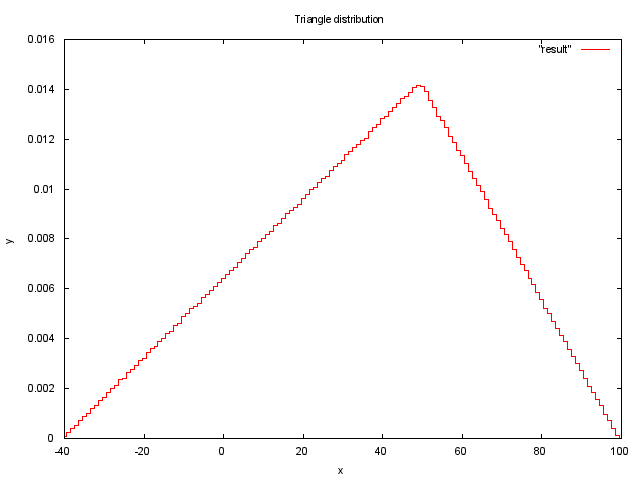
Экспоненциальное распределение

Пусть требуется получить датчик экспоненциально распределенных случайных величин. В этом случае F(x) = 1 – exp(-lambda * x). Тогда из решения уравнения y = 1 – exp(-lambda * x) получаем x = -log(1-y)/lambda.
Можно заметить, что выражение под знаком логарифма в последней формуле имеет равномерное распределение на отрезке [0,1), что позволяет получать другую, но так же распределённую последовательность по формуле: x = -log(y)/lambda, где y есть случайная величина(rand()).

Тесты ГПСЧ

Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.

Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.

В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти тесты DIEHARD и множество других, чтобы определить критостойкость алгоритма.

Что такое ГСЧ – как работает генератор случайных чисел

Генератор случайных чисел, как следует из названия, представляет собой процесс получения случайного числа каждый раз, когда это необходимо, без возможности установить шаблон из ранее сгенерированных чисел. Это число может быть сгенерировано либо алгоритмом, либо аппаратным устройством, и очень важно избежать любого предсказуемого результата.

Алгоритм генератора случайных чисел часто используется в видеоиграх, где он устанавливает разные результаты каждый раз, когда его запускают. Возможно, вы заметили, что даже если вы играете на одном уровне в игре, каждый раз, когда вы пытаетесь выполнить миссию, он не будет одинаковым. Различия не будут наблюдаться в локации или требованиях к миссии, но они будут наблюдаться в количестве приближающихся врагов и областях их появления, изменениях климата и различных препятствиях, которые встречаются между ними. Это делает игру более захватывающей и интересной.

В противном случае, после нескольких попыток игра покажется скучной, так как вы сможете предсказать события, которые произойдут дальше. Это может показаться простым, но для компьютера – генерировать случайные числа – это сложная задача, требующая следовать точным инструкциям, закодированным в нём.

Истинный ГСЧ против псевдо ГСЧ

Есть два типа генераторов случайных чисел: истинные и псевдо.

• Алгоритм истинного генератора случайных чисел создаётся с помощью аппаратного устройства, которое использует очень крошечные физические процессы для генерации случайных чисел. Так как алгоритм не написан; следовательно, истинный ГСЧ не может быть взломан для предсказания. Он обычно используется в системах, ориентированных на безопасность, по всему миру и в некоторых формах шифрования.
• Алгоритм генератора псевдослучайных чисел используется в областях, где нет проблем с безопасностью, а случайность используется, чтобы избежать повторений и сделать что-то более интересное для конечного пользователя. Реализовать технологию дешевле и быстрее, поскольку она не требует оборудования и может быть легко встроена в программный код. Хотя этот процесс не является полностью случайным и определяется на основе алгоритма, он больше подходит для игр и программ.

Какие приложения используют ГСЧ

Не во всех играх используется генератор случайных чисел, что делает их менее конкурентоспособными и часто утомительными, однако, новые игры почти всегда идут с генератором случайных чисел. Многие приложения и игры выигрывают от случайности, поскольку они могут приносить интерес и прибыль только в том случае, если они случайны:

• Азартные игры: бинго, карточные игры, лотереи и подобные игры.
• Игры со сбором добычи: все игры, требующие от игроков сбора добычи для использования в игровом процессе, например, PubG, Diablo и Borderlands используют ГСЧ. Возможность получать лучшую добычу каждый раз – вот причина, по которой люди становятся зависимыми от них.
• Приключенческие игры: такие игры, как Марио и Покемон Го используйте алгоритм генератора случайных чисел, чтобы определить, какие предметы будут добавлены, и каждый раз вы встречайтесь с новым претендентом на покемона.
• Процедурно-сгенерированные игры: все игры, в которых нет предварительно разработанных карт и уровней, но которые были разработаны в игре с использованием процедурного программирования, таких как Minecraft и Civilization. Это помогает создать всю игру с использованием алгоритма.
• Соревновательные игры: некоторые соревновательные игры, например, Counter-Strike используйте алгоритм генератора случайных чисел, чтобы регулировать, как пули поражают цели.

Помимо игровых приложений, есть код случайных чисел в JavaScript, используемый разработчиками и кодировщиками во всём мире для включения генератора случайных чисел в их программы. У Google есть свой очень интересный инструмент, который также основан на теории случайных чисел JavaScript и может генерировать случайные числа. Этот инструмент может пригодиться, когда вы играете в игры с друзьями и семьей. Чтобы посмотреть ГСЧ Google, нажмите здесь.

Манипуляции с ГСЧ

Я уже обсуждал различия между истинным ГСЧ и псевдо ГСЧ и тот факт, что в играх используется псевдо ГСЧ, основанный на алгоритме. Некоторые увлеченные геймеры используют утилиты эмуляции для анализа игр и выявления лазеек, которые можно использовать для управления результатами, даже если используется алгоритм генератора случайных чисел.

ГСЧ на основе алгоритма использует начальное число, которое представляет собой комбинацию определенных факторов и генерирует результат в игре. Это применяемые законы математики, и поскольку 1+1 всегда равно 2, аналогично, если известны факторы в игре, которые приносят желаемый результат, то вы всегда можете достичь того же результата.

Например, если игра требует от игрока выбрать определенного персонажа с определенными усилениями, и результатом будет легкая битва с боссом, то этот шаблон будет постоянным, и все, кто выберет одни и те же варианты, будут иметь одинаковые результаты. Но, для обычного игрока это было бы невозможно, и псевдо-ГСЧ всегда казался бы истинным ГСЧ.

Почему геймеры ненавидят ГСЧ

Геймеров можно разделить на соревнующихся игроков, спидраннеров и средних игроков. Любой конкурентоспособный игрок, овладевший техникой игры и движениями, захочет бросить вызов другим игрокам и побеждать на основе навыков и, несомненно, возненавидит игру, если на результат повлияет генератор случайных чисел. Точно так же спидраннер хотел бы завершить игру как можно скорее, но алгоритм генератора случайных чисел включает тормоза, создавая каждый раз неизвестные и неожиданные сценарии в игре.

В идеале геймеры хотели бы уменьшить количество случаев, когда они сталкиваются со средством генерации случайных чисел в игре, чтобы держать весь игровой процесс и результат под своим контролем. Но, это возможно лишь до определенной степени. И когда геймер часами осваивает игрового персонажа и его движения, он больше всего расстраивается, когда случается что-то случайное, и вся стратегия нарушается. Иногда это тоже действует как благословение, но обычно это проклятие.

Кто такой RNGesus?

Обычные игроки, которые играют только для того, чтобы развлечься или скоротать время, не заботятся о результате игры. Но, опытные профессиональные игроки ненавидят проигрывать только потому, что удача была не в их пользу.

Игроки, которые проигрывают, часто винят в своих поражениях злой ГСЧ, который выгоден их противникам. Там где зло, должен быть Бог – RNGesus.

Среди геймеров во всем мире появился новый термин, RNGesus, который больше соответствует игре слов с «Иисусом». Поскольку Иисус Христос считается нашим спасителем в реальном мире, RNGesus – это вообразимая сущность, созданная для спасения игроков от пагубных последствий ГСЧ. Это нигде не доказывается, но началось как миф, а теперь распространилось по игровому сообществу, как лесной пожар.

Окончательный вердикт по ГСЧ – хорошо или плохо?

На этот вопрос сложно ответить, и определенно не может быть одного и того же ответа для всех. В то время как среднестатистические геймеры утверждают, что это хорошо, другим нравится соревновательный дух.

Алгоритм генератора случайных чисел действительно сохраняет непредсказуемость и интересность каждый раз, когда вы играете на одном уровне. Он стал важной частью многих игр, предлагая разнообразие, например, головоломки, карточные игры, ролевые игры и многие другие. Но, для геймеров, которые верят в навыки как в единственный способ пройти игру, ГСЧ подрывает их потенциал, когда вытаскивает что-то случайное из коробки.

Игры предназначены для развлечения и удовольствия. Если у вас хороший ГСЧ, вы сможете получить лучшие варианты, несмотря на низкие шансы. В случае плохого ГСЧ, вы получите худший результат, даже если вы играли в игру именно так, как должно. Правда в том, что это не то, что можно воспринимать так серьёзно, особенно если оно основано на алгоритме генератора случайных чисел.

Генератор случайных чисел без дубликатов

Рейтинг: 16

Вся проблема в том, что ГенераторСлучайныхЧисел на производительных компьютерах так быстро генерит число, что получается много дубликатов даже в больших числах в конце интервала. Что я имею в виду? Например, мне необходимо было сгенерировать случайным образом 10-ти значные ИНН пусть 20 штук, сделал так:

5555333333
3333333333
3333333333
3333333333
3444444444
4444444444
4999999999
9999999999
9555555555
5555555555
2222222222
2222222222
6666666666
6666666666
2222222222
2222222222
3333333333
3333333333
1111111111
1111111115

Как видите, получилось много дубликатов. В публикации //infostart.ru/public/553616/ говорится о регистре сведений, в котором все хранится и происходит проверка на наличие дублей, я бы тоже использовал такой вариант при необходимости, но мне просто нужно было нагенерить ИНН, и я использовал Массив, в котором проверяю уже существующие коды

8043056388
9102338554
6249282932
1198388359
0526412897
7009103148
0571174217
8993611720
3929803898
7864312503
9471210028
0252270828
4561671060
9351136286
3376451113
7216940055
4858606383
3378262630
6057792110
0900779364

Может, кому-то поможет!

Специальные предложения

Я бы по привычке (с 7.7 начинал) пошел бы списком значений, Отсюда вопрос. Массив быстрее работает чтоли?

И вашем случае я бы чуток по другому сделал

Подробнее, почему у автора так происходит.

У вас инициализация происходит прямо в цикле. За счёт того, что генерация происходит очень быстро, значение ТекущаяУниверсальнаяДатаВМиллисекундах() на следующей итерации такое же как и на предыдущей и получается та же самая последовательность псевдослучайных чисел.
А совет автора из разряда вредных.

Я попробовал два варианта: в одном из них ГСЧ создаётся при открытии формы, а в другом в начале процедуры СлучайныеКоординаты(). Что должно получиться с табличным документом через несколько минут?

Нечто подобное. Такой результат получается если использовать стандартный ГСЧ, или тот что представлен в комментарии (2). Это получается вне зависимости от того, создаём мы генератор при открытии формы, или же каждый раз создаём его при необходимости сгенерировать случайное число. Он привязан к текущей универсальной дате, поэтому я не беспокоюсь об уникальности, ведь он вызывается не чаще 10 раз в секунду. Самое интересное происходит со временем. Вот результат стандартного ГСЧ, который создавался каждый раз при необходимости сгенерировать случайно число, он сдался быстрее всех:

Это тоже стандартный, но генератор был создан единожды при открытии формы. Он продержался дольше

Ниже представлен результат работы ГСЧ из второго комментария, который создавался каждый раз при необходимости получить случайное число. ПРодержался значительно дольше двух предыдущих

И наконец, ГСЧ из второго комментария, который был создан при открытии формы. Продержался дольше всех

Но на этом не заканчиваются фокусы. Когда ломается генератор, ломается интерфейс. Не только платформы, но и винды (во всяком случае семёрки):

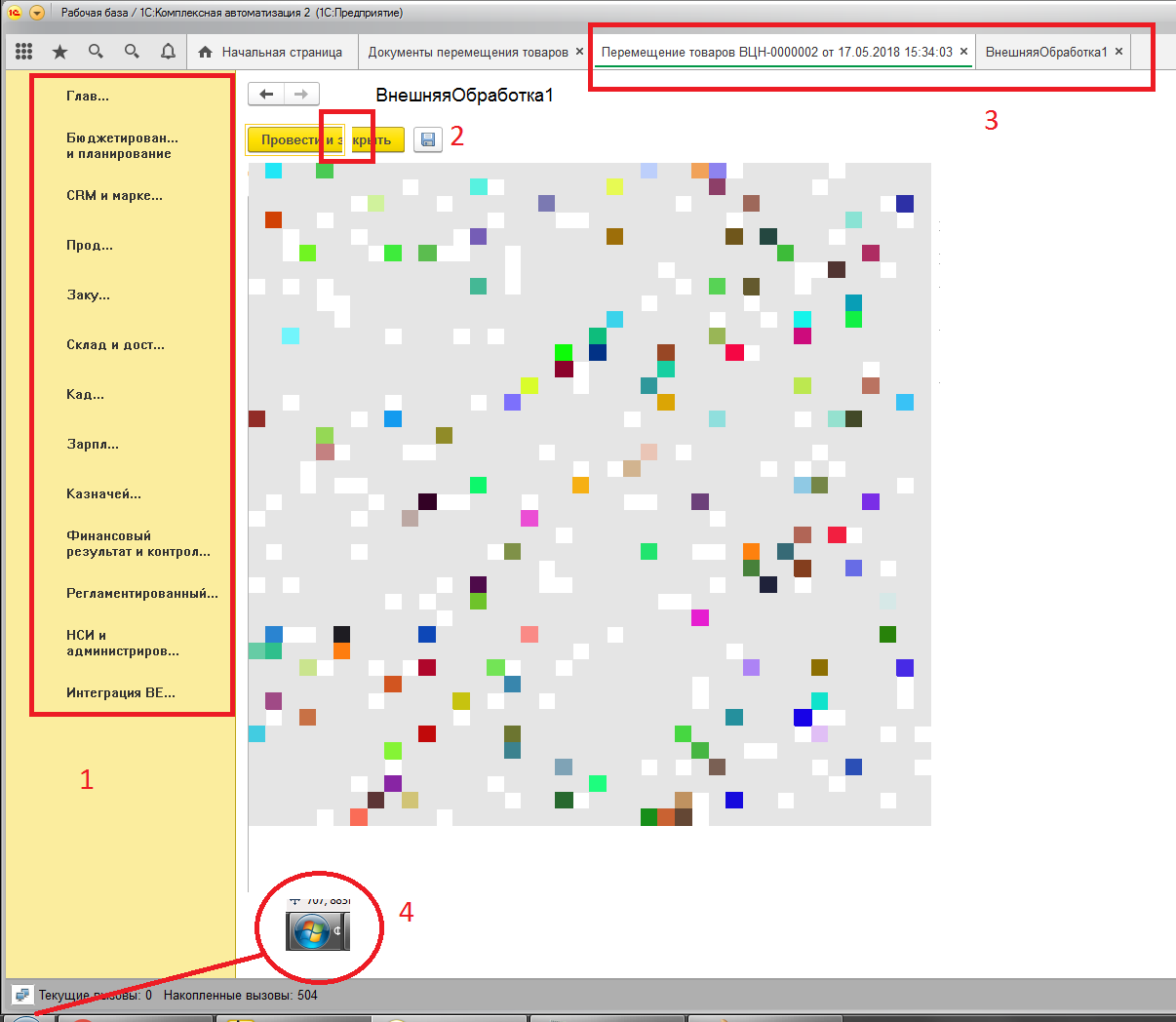
1. Слетают шрифты в панели с подсистемами. Картинки в ней исчезают.
2. В открытой обработке появились кнопки из открытого документа, причём кривые.
3. В то время как открыта обработка, активна вкладка документа, но работать мы можем с обработкой.
4. Ломается кнопка «Пуск».

Интересно, почему всё серое? Диапазон цветов состоит из трёх значений, каждое из которых может быть равно числу от 0 до 255, т.е. всего 256 значений. Серый цвет — это самый усреднённый цвет. Его значение равно 128, 128, 128 (3 раза 256/2). Единственное чего я не понимаю так это почему он стабильно выдаёт среднее значение от 0 до 255, но закрашивает клетки не по диагонали, или не в одном месте.

Можно ли взломать генератор случайных чисел?

Что такое генератор случайных чисел?

Генератор случайных чисел (ГСЧ) – это современный эквивалент бросания кубиков или тасования карт.

В настоящее время эта форма рандомизации математически преобразована в компьютерный алгоритм, который работает для генерации набора случайных чисел, которые (должны) быть свободными от каких-либо шаблонов.

Когда дело доходит до игр казино, лотерей, розыгрышей и подобных игр, ГСЧ принимают форму блоков кода, скрытых в программном обеспечении, которое обеспечивает «шанс» в азартных играх.

Рандомные ГСЧ и псевдо ГСЧ

ГСЧ в играх казино и игровых автоматах на самом деле не рандомные, а скорее «псевдо».

Разница между ними определяется способами, с помощью которых генерируются числа.

В случае радномного ГСЧ генерация чисел обычно является совершенно непредсказуемым физическим явлением (например, радио или атмосферным шумом), питаемым энтропией и объясняемым только с помощью квантовой механики.

П севдо ГСЧ, с другой стороны, используют математический алгоритм или иным образом генерируются компьютером.

Ключевое отличие состоит в том, что с помощью компьютерных алгоритмов весь результат можно было бы технически предсказать, если бы были известны все начальные значения.

Как и во всем, что связано с математикой, если есть уравнение, то оно вовсе не случайное.

Все н е так уж и случайно

Таким образом, несмотря на небольшое неправильное употребление термина «генератор случайных чисел», основная идея остается в том, что все выходные данные будут казаться случайными для любого, кто не знает уравнения или алгоритма.

Правда лишь в том, что большинство ГСЧ не случайны.

Используя уравнение для создания случайных результатов, человек, знакомый с формулой, может фактически предсказать результаты.

Именно эта полуслучайность фактически делает компьютерные ГСЧ уязвимыми для хакеров.

На самом деле есть еще одна причина, по которой ГСЧ может быть только полуслучайным.

Е сли бы ГСЧ действительно работал случайным образом, казино не было довольно шансами игроков.

Поскольку казино – это бизнес, которому необходимо получать прибыль, чтобы быть на плаву, ГСЧ должны быть запрограммированы соответствующим образом.

Однако этот процесс незначительного уравновешивания шансов в пользу казино открывает слабое место для потенциальной атаки.

Итак, можно ли взломать ГСЧ?

Генераторы случайных чисел довольно сложны.

Как видите, они включают в себя сложный математический код, который скрыт в программном обеспечении, зашифрован и спрятан в компьютерах, за которыми следят камеры видеонаблюдения.

Вы должны быть полным идиотом, если думаете, что можете взломать Генератор случайных чисел.

Фактически, вам действительно нужна лишь небольшая часть информации, чтобы взломать этот код.

Поскольку ГСЧ – это в основном повторные вызовы функций для генерации «случайных» чисел, все, что вам нужно, это ключ к функции.

Подобно шифру, используемому для декодирования секретного сообщения, знание критического «ключа» – это то, что может позволить вам взломать код.

Это число, также известное как «начальное число», представляет собой начальное целое число, которое вставляется в ГСЧ, с которого начинается вся операция.

Как только вы нашли семя, весь алгоритм можно легко расшифровать.

Если хакер может заменить псевдослучайный бит предсказуемым способом, краткий ответ заключается в том, что безопасность ГСЧ полностью скомпрометирована (и обычно не обнаруживается).

Но, легче сказать, чем сделать.

Есть несколько ярких примеров успешного взлома ГСЧ различными способами.

Некоторые атаки успешны с помощью реверс-инжиниринга, а некоторые системные взломы являются случайными, когда недостатки (или ошибки) в коде непреднамеренно раскрывают ключ к любопытным глазам.

Заключение

Как видите, вполне возможно взломать ГСЧ, основанный на компьютерных программах, подобных тем, которые используются в казино и онлайн-играх.

Однако нельзя сказать, что это легко.

Эти компании тратят немалые деньги, чтобы убедиться, что их игры безопасны!

Компании, использующие программное обеспечение ГСЧ, также применяют множество защитных стратегий, таких как шифрование, аппаратное обеспечение безопасности, потоковые шифры и сменные ключи.

Даже опытные хакеры могут столкнуться со сложностями взлома такого программного обеспечения, что делает вероятность внешней атаки довольно минимальной.

Как компьютер генерирует случайные числа

Что такое случайность в компьютере? Как происходит генерация случайных чисел? В этой статье мы постарались дать простые ответы на эти вопросы.

В программном обеспечении, да и в технике в целом существует необходимость в воспроизводимой случайности: числа и картинки, которые кажутся случайными, на самом деле сгенерированы определённым алгоритмом. Это называется псевдослучайностью, и мы рассмотрим простые способы создания псевдослучайных чисел. В конце статьи мы сформулируем простую теорему для создания этих, казалось бы, случайных чисел.

Определение того, что именно является случайностью, может быть довольно сложной задачей. Существуют тесты (например, колмогоровская сложность), которые могут дать вам точное значение того, насколько случайна та или иная последовательность. Но мы не будем заморачиваться, а просто попробуем создать последовательность чисел, которые будут казаться несвязанными между собой.

Часто требуется не просто одно число, а несколько случайных чисел, генерируюемых непрерывно. Следовательно, учитывая начальное значение, нам нужно создать другие случайные числа. Это начальное значение называется семенем, и позже мы увидим, как его получить. А пока давайте сконцентрируемся на создании других случайных значений.

Создание случайных чисел из семени

Один из подходов может заключаться в том, чтобы применить какую-то безумную математическую формулу к семени, а затем исказить её настолько, что число на выходе будет казаться непредсказуемым, а после взять его как семя для следующей итерации. Вопрос только в том, как должна выглядеть эта функция искажения.

Давайте поэкспериментируем с этой идеей и посмотрим, куда она нас приведёт.

Функция искажения будет принимать одно значение, а возвращать другое. Назовём её R.

Начнём с того, что R — это простая функция, которая всего лишь прибавляет единицу.

Если значение нашего семени 1, то R создаст ряд 1, 2, 3, 4, . Выглядит совсем не случайно, но мы дойдём до этого. Пусть теперь R добавляет константу вместо 1.

Если с равняется, например, 7, то мы получим ряд 1, 8, 15, 22, . Всё ещё не то. Очевидно, что мы упускаем то, что числа не должны только увеличиваться, они должны быть разбросаны по какому-то диапазону. Нам нужно, чтобы наша последовательность возвращалась в начало — круг из чисел!

Числовой круг

Посмотрим на циферблат часов: наш ряд начинается с 1 и идёт по кругу до 12. Но поскольку мы работаем с компьютером, пусть вместо 12 будет 0.

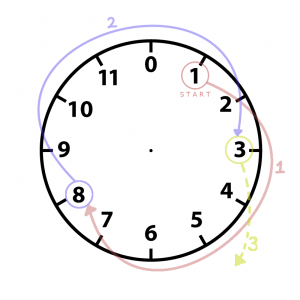
Теперь начиная с 1 снова будем прибавлять 7. Прогресс! Мы видим, что после 12 наш ряд начинает повторяться, независимо от того, с какого числа начать.

Здесь мы получаем очень важно свойство: если наш цикл состоит из n элементов, то максимальное число элементов, которые мы можем получить перед тем, как они начнут повторяться это n.

Теперь давайте переделаем функцию R так, чтобы она соответствовала нашей логике. Ограничить длину цикла можно с помощью оператора модуля или оператора остатка от деления.

На этом этапе вы можете заметить, что некоторые числа не подходят для c. Если c = 4, и мы начали с 1, наша последовательность была бы 1, 5, 9, 1, 5, 9, 1, 5, 9, . что нам конечно же не подходит, потому что эта последовательность абсолютно не случайная. Становится понятно, что числа, которые мы выбираем для длины цикла и длины прыжка должны быть связаны особым образом.

Если вы попробуете несколько разных значений, то сможете увидеть одно свойство: m и с должны быть взаимно простыми.

До сих пор мы делали «прыжки» за счёт добавления, но что если использовать умножение? Умножим х на константу a.

Свойства, которым должно подчиняться а, чтобы образовался полный цикл, немного более специфичны. Чтобы создать верный цикл:

1. (а — 1) должно делиться на все простые множители m
2. (а — 1) должно делиться на 4, если m делится на 4

Эти свойства вместе с правилом, что m и с должны быть взаимно простыми составляют теорему Халла-Добелла. Мы не будем рассматривать её доказательство, но если бы вы взяли кучу разных значений для разных констант, то могли бы прийти к тому же выводу.

Выбор семени

Настало время поговорить о самом интересном: выборе первоначального семени. Мы могли бы сделать его константой. Это может пригодиться в тех случаях, когда вам нужны случайные числа, но при этом нужно, чтобы при каждом запуске программы они были одинаковые. Например, создание одинаковой карты для каждой игры.

Еще один способ — это получать семя из нового источника каждый раз при запуске программы, как в системных часах. Это пригодится в случае, когда нужно общее рандомное число, как в программе с бросанием кубика.

Конечный результат

Когда мы применяем функцию к её результату несколько раз, мы получаем рекуррентное соотношение. Давайте запишем нашу формулу с использованием рекурсии:

Где начальное значение х — это семя, а — множитель, с — константа, m — оператор остатка от деления.

То, что мы сделали, называется линейным конгруэнтным методом. Он очень часто используется, потому что он прост в реализации и вычисления выполняются быстро.

В разных языках программирования реализация линейного конгруэнтного метода отличается, то есть меняются значения констант. Например, функция случайных чисел в libc (стандартная библиотека С для Linux) использует m = 2 ^ 32, a = 1664525 и c = 1013904223. Такие компиляторы, как gcc, обычно используют эти значения.

Заключительные замечания

Существуют и другие алгоритмы генерации случайных чисел, но линейный конгруэнтный метод считается классическим и лёгким для понимания. Если вы хотите глубже изучить данную тему, то обратите внимание на книгу Random Numbers Generators, в которой приведены элегантные доказательства линейного конгруэнтного метода.

Генерация случайных чисел имеет множество приложений в области информатики и особенно важна для криптографии.

random – Генераторы псевдослучайных чисел

Автор: Doug Hellmann
Дата записи

Реализует несколько типов генераторов псевдослучайных чисел.

Модуль random предоставляет быстрый генератор псевдослучайных чисел на основе алгоритма Mersenne Twister . Первоначально разработанный для создания входных данных для моделирования методом Монте-Карло, Mersenne Twister генерирует числа с почти равномерным распределением и большим периодом, что делает его пригодным для широкого круга приложений.

Генерация случайных чисел

Функция random () возвращает следующее случайное значение с плавающей запятой из сгенерированной последовательности. Все возвращаемые значения попадают в диапазон 0 n .

Повторный запуск программы дает разные последовательности чисел.

Чтобы сгенерировать числа в определенном числовом диапазоне, используйте вместо этого uniform () .

Передайте минимальное и максимальное значения, и uniform () настроит возвращаемые значения из random () , используя формулу min + (max — min) * random () .

Посев

random () выдает разные значения каждый раз при вызове и имеет очень большой период перед повторением любых чисел. Это полезно для получения уникальных значений или вариаций, но иногда бывает полезно иметь один и тот же набор данных, который можно обрабатывать разными способами. Один из способов – использовать программу для генерации случайных значений и сохранения их для обработки на отдельном этапе. Однако это может оказаться непрактичным для больших объемов данных, поэтому random включает функцию seed () для инициализации генератора псевдослучайных чисел, чтобы он генерировал ожидаемый набор значений.

Начальное значение управляет первым значением, созданным формулой, используемой для создания псевдослучайных чисел, и, поскольку формула является детерминированной, она также устанавливает полную последовательность, полученную после изменения начального числа. Аргументом для seed () может быть любой хешируемый объект. По умолчанию используется зависящий от платформы источник случайности, если он доступен. В противном случае используется текущее время.

Состояние сохранения

Внутреннее состояние псевдослучайного алгоритма, используемого random () , можно сохранить и использовать для управления числами, полученными в последующих запусках. Восстановление предыдущего состояния перед продолжением снижает вероятность повторения значений или последовательностей значений из более раннего ввода. Функция getstate () возвращает данные, которые можно использовать для повторной инициализации генератора случайных чисел позже с помощью setstate () .

Данные, возвращаемые функцией getstate () , являются деталью реализации, поэтому в этом примере данные сохраняются в файл с помощью pickle, но в остальном они рассматриваются как черный ящик. Если файл существует при запуске программы, он загружает старое состояние и продолжает работу. Каждый прогон производит несколько чисел до и после сохранения состояния, чтобы показать, что восстановление состояния заставляет генератор снова выдавать те же значения.

Случайные целые числа

random () генерирует числа с плавающей запятой. Можно преобразовать результаты в целые числа, но использование randint () для генерации целых чисел напрямую более удобно.

Аргументы для randint () – это концы включающего диапазона значений. Числа могут быть положительными или отрицательными, но первое значение должно быть меньше второго.

randrange () – это более общая форма выбора значений из диапазона.

randrange () поддерживает аргумент step в дополнение к значениям start и stop, поэтому он полностью эквивалентен выбору случайного значения из диапазона (start, stop, шаг) . Это более эффективно, потому что диапазон фактически не строится.

Выбор случайных предметов

Генераторы случайных чисел часто используют для выбора случайного элемента из последовательности пронумерованных значений, даже если эти значения не являются числами. random включает функцию choice () для выполнения случайного выбора из последовательности. В этом примере имитируется подбрасывание монеты 10 000 раз, чтобы подсчитать, сколько раз выпадает орел, а сколько решка.

Допускаются только два результата, поэтому вместо использования чисел и их преобразования в choice () используются слова «орла» и «решка». Результаты заносятся в таблицу с использованием имен результатов в качестве ключей.

Перестановки

При моделировании карточной игры необходимо перемешать колоду карт и затем раздать их игрокам, не используя одну и ту же карту более одного раза. Использование choice () может привести к тому, что одна и та же карта будет сдана дважды, поэтому вместо этого колоду можно смешивать с помощью shuffle () , а затем удалять отдельные карты по мере их раздачи.

Карты представлены в виде строк с номиналом и буквой, обозначающей масть. Сданные «руки» создаются путем добавления по одной карте в каждый из четырех списков и удаления ее из колоды, чтобы ее нельзя было раздать снова.

Отбор проб

Для многих моделей необходимы случайные выборки из совокупности входных значений. Функция sample () генерирует образцы без повторения значений и без изменения входной последовательности. В этом примере печатается случайная выборка слов из системного словаря.

Алгоритм создания набора результатов учитывает размеры входных данных и запрашиваемой выборки, чтобы получить результат как можно более эффективно.

Несколько одновременных генераторов

В дополнение к функциям на уровне модуля random включает класс Random для управления внутренним состоянием нескольких генераторов случайных чисел. Все функции, описанные ранее, доступны как методы экземпляров Random , и каждый экземпляр можно инициализировать и использовать отдельно, не влияя на значения, возвращаемые другими экземплярами.

В системе с хорошим естественным заполнением случайных значений экземпляры запускаются в уникальных состояниях. Однако, если нет хорошего генератора случайных значений платформы, экземпляры, вероятно, были заполнены текущим временем и, следовательно, производят те же значения.

SystemRandom

Некоторые операционные системы предоставляют генератор случайных чисел, который имеет доступ к большему количеству источников энтропии, которые могут быть введены в генератор. random предоставляет эту функцию через класс SystemRandom , который имеет тот же API, что и Random , но использует os.urandom () для генерации значений, которые составляют основу всех других алгоритмов.

Последовательности, созданные SystemRandom , не воспроизводятся, поскольку случайность исходит от системы, а не от состояния программного обеспечения (фактически, seed () и setstate () не имеют никакого эффекта).

Неравномерные распределения

В то время как равномерное распределение значений, создаваемых random () , полезно для множества целей, другие распределения более точно моделируют конкретные ситуации. Модуль random также включает функции для создания значений в этих распределениях. Они перечислены здесь, но не рассматриваются подробно, поскольку их использование, как правило, является специализированным и требует более сложных примеров.

Нормальный

нормальное распределение обычно используется для неоднородных непрерывных значений, таких как классы, высота, веса и т. Д. Кривая, полученная с помощью распределения, имеет характерную форму, которая привела к тому, что ее называют “колоколообразной кривой”. ” random включает две функции для генерации значений с нормальным распределением, normalvariate () и немного более быструю gauss () (нормальное распределение также называется распределение Гаусса).

Связанная функция lognormvariate () создает псевдослучайные значения, в которых логарифм значений распределяется нормально. Логнормальные распределения полезны для значений, которые являются продуктом нескольких случайных величин, которые не взаимодействуют.

Приближение

треугольное распределение используется как приблизительное распределение для небольших выборок. «Кривая» треугольного распределения имеет низкие точки при известных минимальных и максимальных значениях и максимальную точку в режиме, который оценивается на основе «наиболее вероятного» результата (отраженного аргументом режима в triangular () ).

Экспоненциальный

expovariate () создает экспоненциальное распределение, полезное для моделирования значений времени прибытия или интервалов для однородных пуассоновских процессов, таких как скорость радиоактивного распада или запросы, поступающие на веб-сервер.

Распределение Парето, или степенной закон, соответствует многим наблюдаемым явлениям и было популяризировано изданием Длинный хвост Криса Андерсона. Функция paretovariate () полезна для моделирования распределения ресурсов между людьми (богатство людям, спрос на музыкантов, внимание к блогам и т. Д.).

Угловой

Распределение фон Мизеса, или круговое нормальное распределение (создается с помощью vonmisesvariate () ), используется для вычисления вероятностей циклических значений, таких как углы, календарные дни и время.

Размеры

betavariate () генерирует значения с бета-распределением, которое обычно используется в байесовской статистике и приложениях, таких как моделирование продолжительности задач.

Гамма-распределение, создаваемое gammavariate () , используется для моделирования размеров таких вещей, как время ожидания, количество осадков и вычислительные ошибки.

Распределение Вейбулла, вычисленное с помощью weibullvariate () , используется в анализе отказов, промышленной инженерии и прогнозировании погоды. Он описывает распределение размеров частиц или других дискретных объектов.

• Стандартная библиотека документации для случайного выбора
• «Мерсенн Твистер: генератор равномерных псевдослучайных чисел с 623-мерным распределением» – статья М. Мацумото и Т. Нишимура из Транзакции ACM по моделированию и компьютерному моделированию Vol. 8, No. 1, январь, стр. 3-30 1998.
• Wikipedia: Mersenne Twister – статья об алгоритме псевдослучайного генератора, используемом Python.
• Википедия: Равномерное распределение – статья о непрерывных равномерных распределениях в статистике.